1268 Пусть А и B — данные точки, k — данное положительное число, не равное 1. а) Докажите, что множество всех точек М, удовлетворяющих условию АМ=kBM, есть окружность (окружность Аполлония). б) Докажите, что эта окружность пересекается с любой окружностью, проходящей через точки А и B, так, что их радиусы, проведенные в точку пересечения, взаимно перпендикулярны.

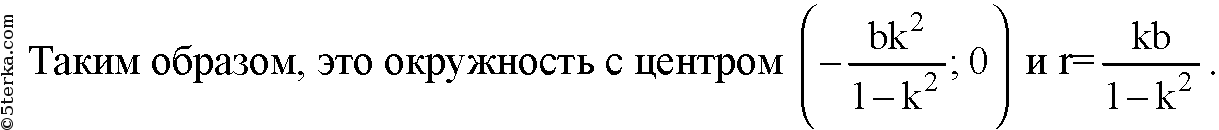

Источник:
 Решебник
по
геометрии
за 9 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2005 год),
Решебник
по
геометрии
за 9 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2005 год),
задача №1268
к главе «Задачи повышенной трудности. Задачи к главе X».
Комментарии