579. Докажите, что каждое из следующих уравнений является уравнением сферы. Найдите координаты центра и радиус этой сферы: а) х2 —4x + y2 + z2 =0; б) x2+y2+z2—2y= 24; в) х2+ 2х + у2+z2 = 3; г) х2 — х — y2 + 3y + z2 —2z = 2,5.
а)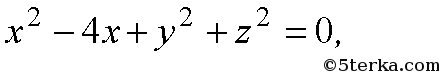

- уравнение сферы.
Координаты центра (2; 0; 0), радиус: 2;
б)
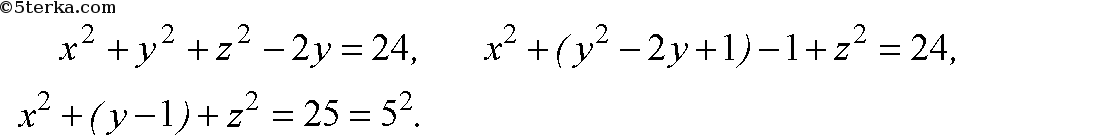
Координаты центра (0; 1; 0), радиус: 5;
в)

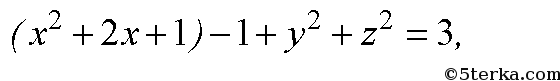

— уравнение сферы с центром (01; 0; 0), радиус: 2;
г)

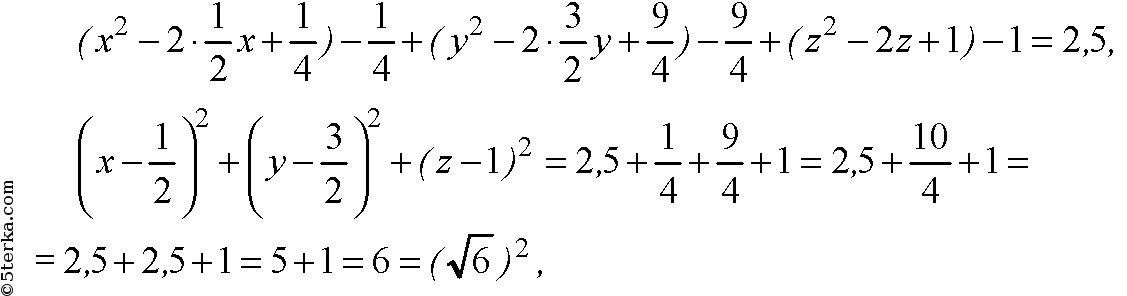

— уравнение сферы; в точке с координатами

расположен ее центр, радиус равен √6.
Источник:
 Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №579
к главе «Глава VI. Цилиндр, конус и шар § 3. Сфера».
Комментарии