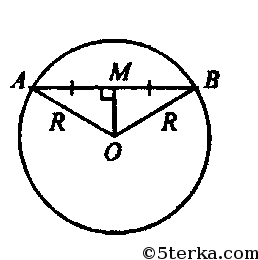
— центр сферы. В сечении получим окружность радиуса R, проходящая через центр сферы. В равнобедренном ΔOAB проведем ОМ⊥АВ. ОМ — высота в равнобедренном треугольнике, таким образом, ОМ — медиана,

ОМ — искомое расстояние.

Источник:
 Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №575
к главе «Глава VI. Цилиндр, конус и шар § 3. Сфера».
Комментарии