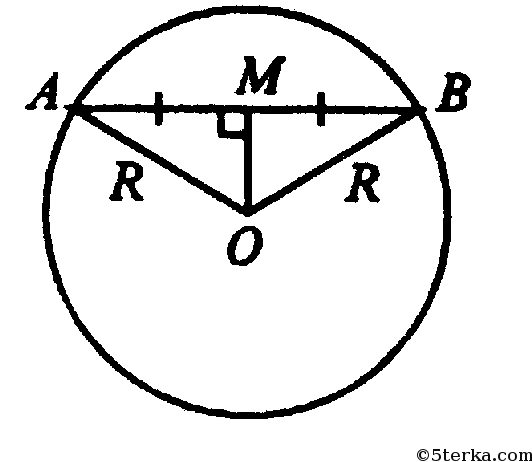
574. Точка М — середина отрезка АВ, концы которого лежат на сфере радиуса R с центром О. Найдите: а) ОМ, если R = 50 см, AB=40 см; б) ОМ, если R = 15 мм, АВ= 18 мм; в) АВ, если R=10 дм, ОМ =60 см; г) AM, если R=a, ОМ = b.

Проведем секущую плоскость через точки А, В и О. Сечение серы этой плоскостью будет окружностью радиуса R с центром в точке О. ОМ — медиана в равнобедренном ΔАОВ, поэтому ОМ⊥АВ.

а)

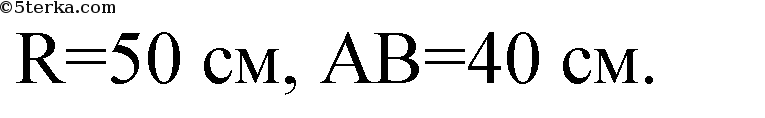
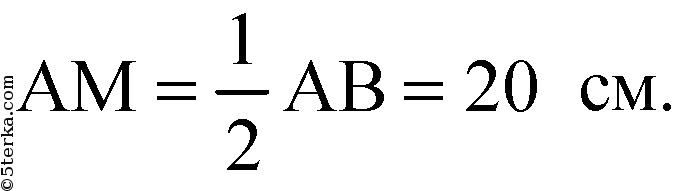
Из ΔАОМ:

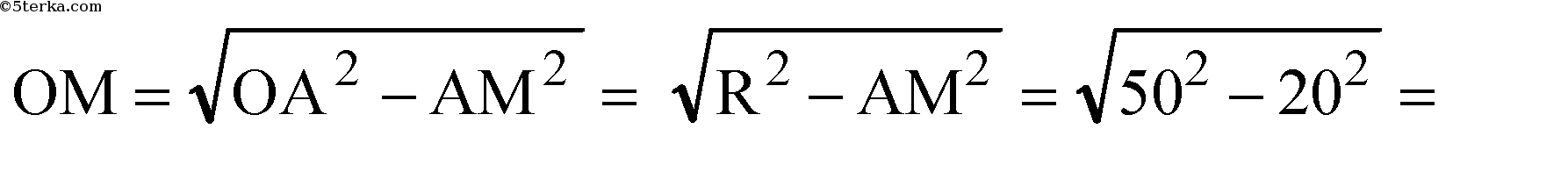
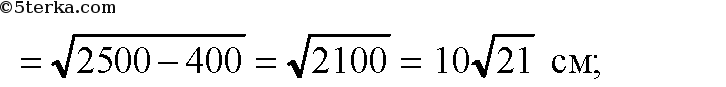
б)

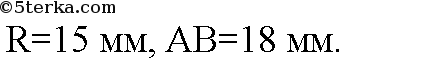
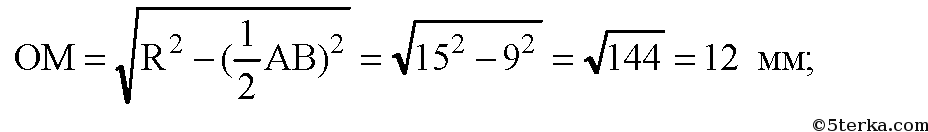
в)

R=10 дм, ОМ=60 см, найти АВ. ОМ=60 см=6 дм.

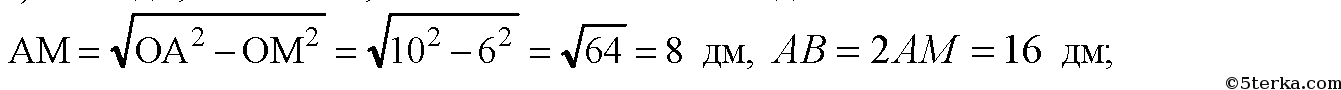
г) R=а, ОМ=b.

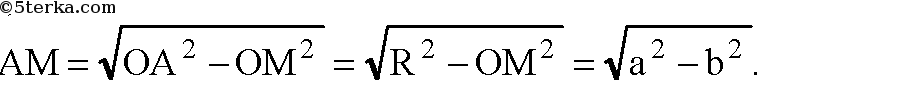
Источник:

Решебник по геометрии за 10 класс к учебнику Геометрия. 10-11 класс Л.С.Атанасян Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №574
к главе «Глава VI. Цилиндр, конус и шар § 3. Сфера».

Все задачи

← 573. Точки А и В лежат на сфере с центром O∉АВ, а точка М лежит на отрезке АВ. Докажите, что: а) если М — середина отрезка АВ, то ОМ⊥АВ; б) если ОМ⊥АВ, то М — середина отрезка АВ.
575. Точки А и В лежат на сфере радиуса R. Найдите расстояние от центра сфера до прямой АВ, если АВ = m. →
Комментарии