177. Докажите, что плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.

* В задачах этого параграфа двугранный угол с ребром АВ, на разных гранях которого отмечены точки С и D, для краткости будем называть так: двугранный угол CABD.

Решение:

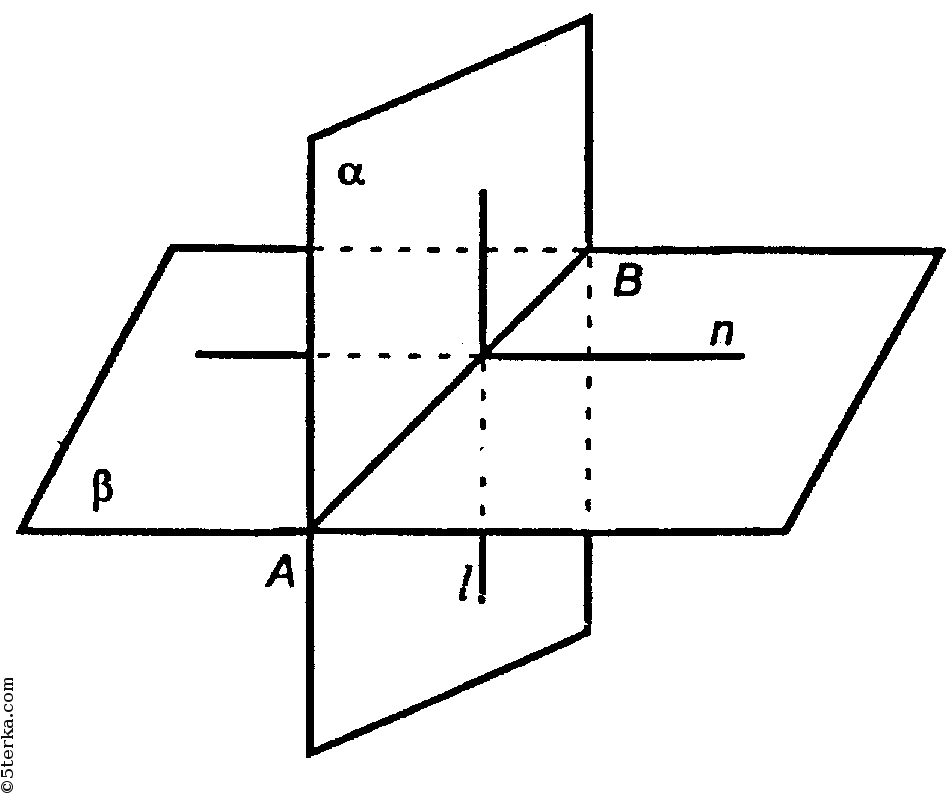
Пусть α и β пересекаются по линии АВ, γ ⊥ АВ (на рисунке не показана).

АВ ⊥ γ, АВ ⊂ α, то по теореме п. 23 γ ⊥ α.

АВ ⊥ γ, АВ ⊂ β, то по теореме п. 23 γ ⊥ β.

Что и требовалось доказать.