171. Гипотенуза прямоугольного равнобедренного треугольника лежит в плоскости а, а катет наклонен к этой плоскости под углом 30°. Найдите угол между плоскостью α и плоскостью треугольника.

* В задачах этого параграфа двугранный угол с ребром АВ, на разных гранях которого отмечены точки С и D, для краткости будем называть так: двугранный угол CABD.

Дано:

Решение:

Проведем СО ⊥ α; проведем отрезки ОА и ОВ.

(по условию), т.к. это и есть угол между катетом и

плоскостью а.

(катет, лежащий против

угла 30о, равен половине гипотенузы).

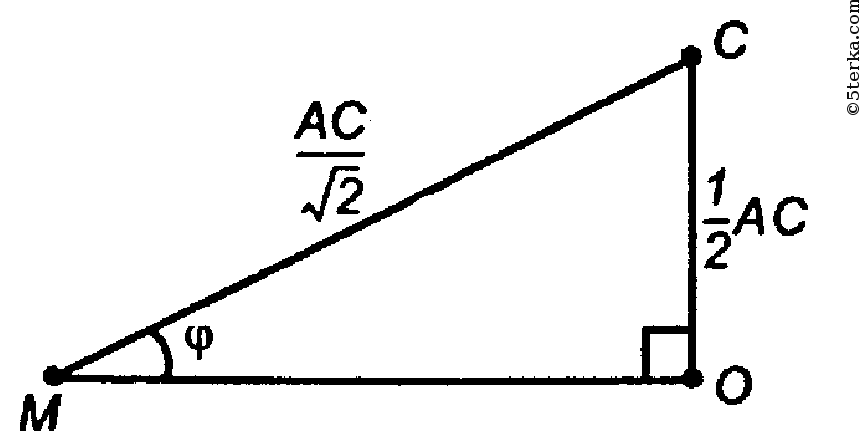
Проведем ОМ ⊥ АВ.

то по теореме о 3-х перпендикулярах СМ ⊥ АВ.

Из ΔАМС:

- линейный угол двугранного угла.

- прямоугольный, т.е.

(φ ≠ 135о, так как ΔСМО - прямоугольный).

Ответ: 45о.

Источник:

Решебник по геометрии за 10 класс к учебнику Геометрия. 10-11 класс Л.С.Атанасян Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №171
к главе «Глава II Перпендикулярность прямых и плоскостей. §3 Двугранный угол. Перпендикулярность плоскостей.».

Все задачи

← 170. Из вершины В треугольника ABC, сторона АС которого лежит в плоскости а, проведен к этой плоскости перпендикуляр BB1. Найдите расстояния от точки В до прямой АС и до плоскости α, если АВ = 2 см, ∠ВАС= 150° и двугранный угол ВАСВ1 равен 45°.
172. Катет АС прямоугольного треугольника ABC с прямым углом С лежит в плоскости α, а угол между плоскостями α и ABC равен 60°. Найдите расстояние от точки В до плоскости α, если АС = 5 см, АВ = 13 см. →
Комментарии