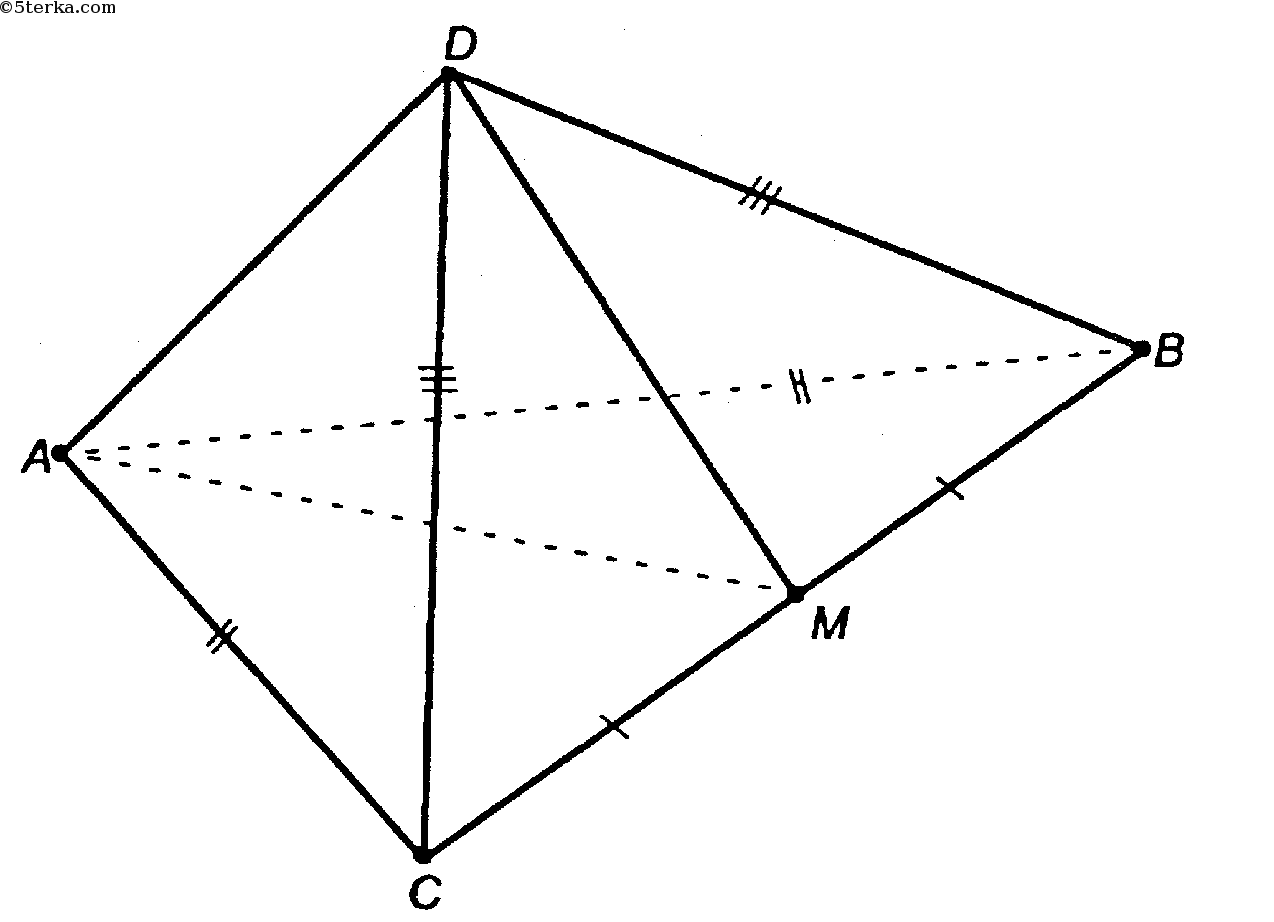
131. В тетраэдре ABCD точка М — середина ребра ВС, АВ = AC, DB = DC. Докажите, что плоскость треугольника ADM перпендикулярна к прямой ВС.

Дано:

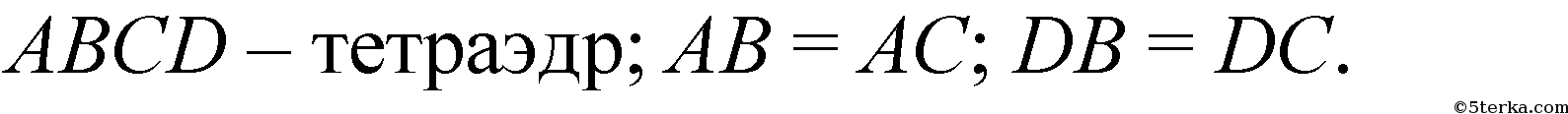
Решение:

ΔАВС - равнобедренный, АМ - медиана, то и высота, то есть АМ ⊥ ВС.

ΔDCB - равнобедренный, DM - медиана, то и высота, то есть DM ⊥ BC.

Т.к. MD и МА пересекаются, то по признаку перпендикулярности прямой и плоскости СВ ⊥ пл. AMD.

Что и требовалось доказать.

Источник:

Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №131
к главе «Глава II Перпендикулярность прямых и плоскостей. §1 Перпендикулярность прямой и плоскости».

Все задачи

← 130. Через вершину В квадрата ABCD проведена прямая ВМ. Известно, что ∠MBA = ∠MBC=90°, МВ =m, АВ = n. Найдите расстояния от точки М до: а) вершин квадрата; б) прямых АС и BD.

132. Докажите, что если одна из двух параллельных плоскостей перпендикулярна к прямой, то и другая плоскость перпендикулярна к этой прямой. →

Комментарии