103. На ребрах DA, DB и DC тетраэдра DABC отмечены точки М, N и Р так, что DM:MA = DN:NB = DP:PC. Докажите, что плоскости MNP и ABC параллельны. Найдите площадь треугольника MNP, если площадь треугольника ABC равна 10 см2 и DM: МА = 2:1.

Рассмотрим ΔADC и ΔMDP.

Из условия

но

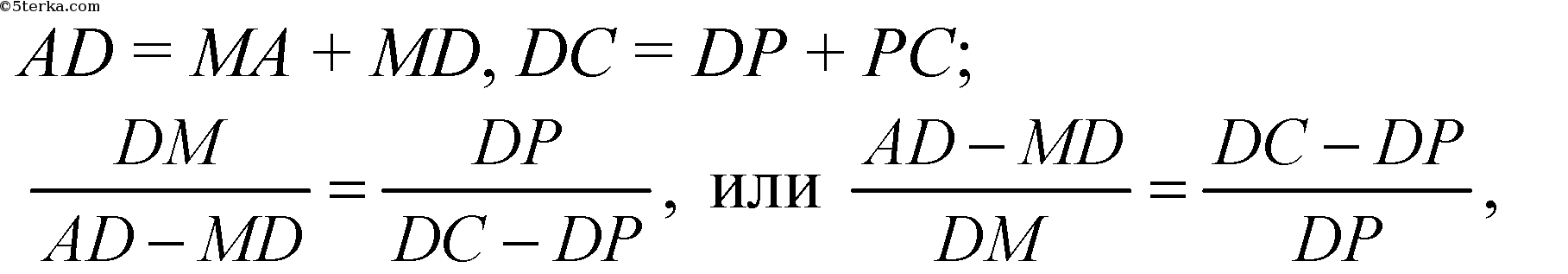
отсюда

Так как у ΔADC и ΔMDP угол D - общий, а стороны, образующие ∠D - пропорциональны, значит, ΔADC ~ ΔMDP.

Из подобия следует:

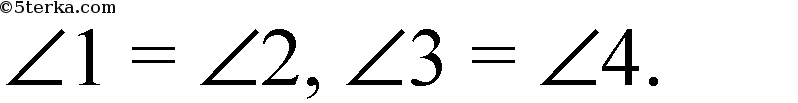
Из равенства углов получим, что МР || AC.

Аналогично, для грани DCB, имеем, что PN || CB.

Итак, MP || AC и PN || CB. По теореме п. 10 пл. MNP || пл. ABC. ΔMNP ~ ΔABC (по двум углам).

или

Раз

то

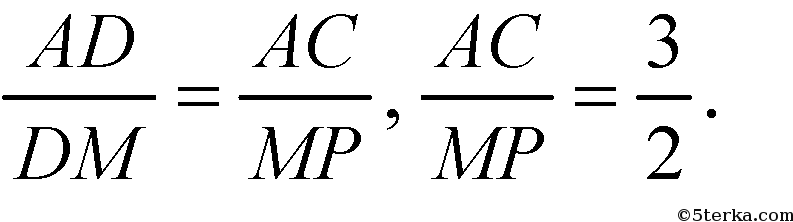
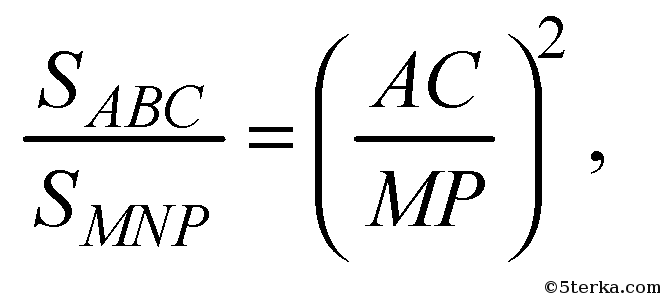
т.к. площади подобных фигур относятся как

квадраты линейных размеров.

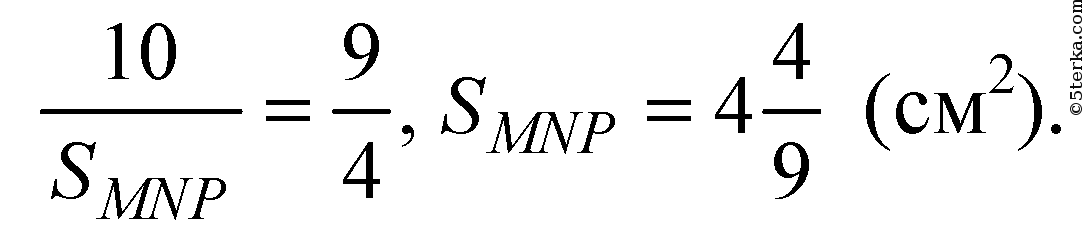
Ответ: