104. Изобразите тетраэдр ABCD и отметьте точку М на ребре АВ. Постройте сечение тетраэдра плоскостью, проходящей через точку М параллельно прямым АС и BD.

Проведем ME || AC и MF || BD.

По теореме II плоскость сечения пересечет пл. BCD по прямой, параллельной MF (MF || пл. BCD по построению), значит, проводим EK || BD. Соединим точки K и F.

4-угольник MEKF - искомое сечение. Докажем это.

Итак,

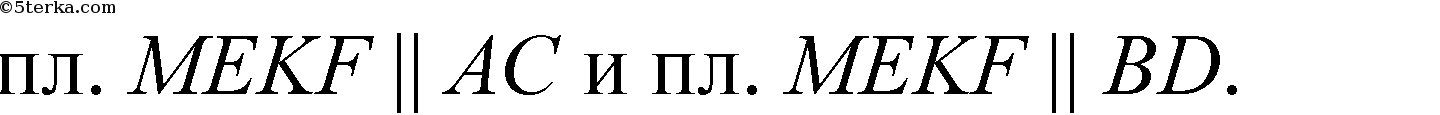
Так как через т. М можно провести лишь одну прямую ME || AC в плоскости грани АВС и одну прямую MF || BD в плоскости грани BAD, то плоскость MEKF - единственная, удовлетворяющая условию задачи.

Источник:

Решебник по геометрии за 10 класс к учебнику Геометрия. 10-11 класс Л.С.Атанасян Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №104
к главе «Дополнительные задачи к главе I Параллельность прямых и плоскостей.».

Все задачи

← 103. На ребрах DA, DB и DC тетраэдра DABC отмечены точки М, N и Р так, что DM:MA = DN:NB = DP:PC. Докажите, что плоскости MNP и ABC параллельны. Найдите площадь треугольника MNP, если площадь треугольника ABC равна 10 см2 и DM: МА = 2:1.
105. Изобразите тетраэдр DABС и отметьте точки М и N на ребрах BD и CD и внутреннюю точку К грани ABC. Постройте сечение тетраэдра плоскостью MNK. →
Комментарии