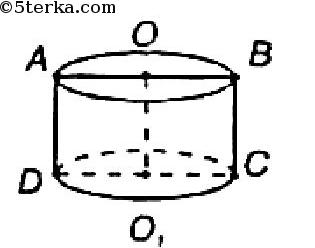
Так как ОBСО1 — квадрат, то высота цилиндра ОО1 равна радиусу основания ОВ. Площадь поверхности цилиндра равна сумме площадей боковой поверхности и двух оснований:
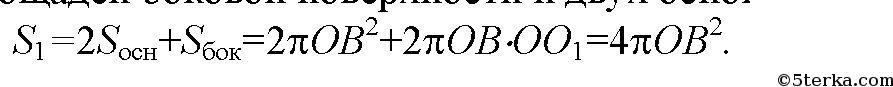
Далее, площадь поверхности шара, имеющего радиусом стороДалее, площадь поверхности шара, имеющего радиусом сторону основания, равна
ну основания, равна
Что и требовалось докаЧто и требовалось доказать.
Источник:
Решебник
по
геометрии
за 11 класс (А.В. Погорелов, 2001 год),
задача №35
к главе «§ 23. Объемы и поверхности тел вращения».
Комментарии