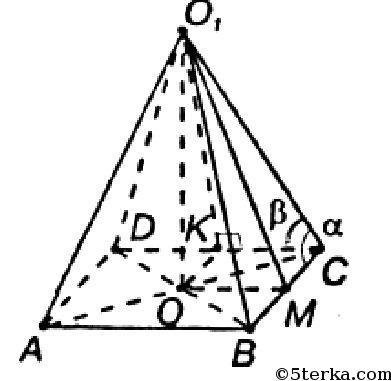
42. В основании пирамиды лежит прямоугольник. Каждое боковое ребро пирамиды равно l и составляет со смежными сторонами прямоугольника углы α и β. Найдите объем пирамиды.

Так как все боковые ребра пирамиды равны, то ее высота OO1 проходит через центр описанной около основания окружности. Центр окружности, описанной около прямоугольника, это точка пересечения диагоналей. Так что

чения диагоналей. Так что

Проведем O1M⊥BC и

O1K⊥DC. Тогда по теореме о трех перпендикулярах OM⊥BC, a OK⊥DC. Так что ОМСК — прямоугольник и ОМ=КС. В прямоугольных ΔO1CM и ΔO1CK: CM=O1C⋅cosα=l⋅cosα, KC=O1C⋅cosβ=l⋅cosβ.

Далее, в прямоугольном ΔОСМ по теореме Пифагора:

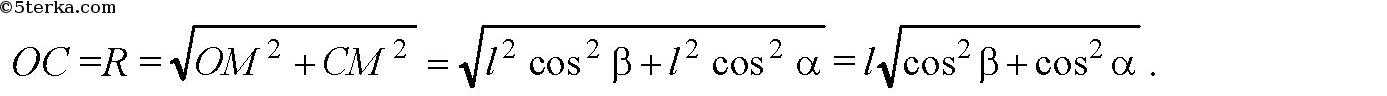
Далее, в прямоугольном ΔO1OC:

Затем площадь основания

Источник:

Домашняя работа по геометрии за 11 класс к учебнику «Геометрия. 10-11 класс» А.В. Погорелов Решебник по геометрии за 11 класс (А.В. Погорелов, 2001 год),
задача №42
к главе «§22. Объемы многогранников».

Все задачи

← 40. Основание пирамиды — равнобедренный треугольник со сторонами 6 см, 6 см и 8 см. Все боковые ребра равны 9 см. Найдите объем пирамиды.
43. Найдите объем пирамиды, имеющий основанием треугольник, два угла которого α и β; радиус описанного круга R. Боковые ребра пирамиды наклонены к плоскости ее основания под углом у. →
Комментарии