Проведем высоту пирамиды O1O. В правильной пирамиде высота проходит через центр окружности, вписанной в основание. Тогда проведем ОЕ⊥АВ. По теореме о трех перпендикулярах O1Е⊥АВ. Так что ОЕ — радиус вписанной окружности, а ∠O1EO=45° как линейный угол данного двугранного угла.
Тогда
Далее в ΔО1ОЕ:
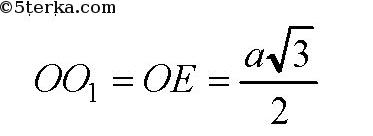
(так как ΔО1ОЕ — равнобедренный).
Далее площадь основания равна площади 6 равносторонних треугольников со стороной а:
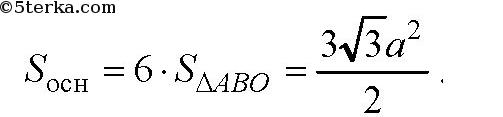
Так что
Источник:
Решебник
по
геометрии
за 11 класс (А.В. Погорелов, 2001 год),
задача №34
к главе «§22. Объемы многогранников».
Комментарии