33. По стороне основания а и боковому ребру b найдите объем правильной пирамиды: 1) треугольной, 2) четырехугольной, 3) шестиугольной.

В правильной пирамиде высота проходит через центр окружности, описанной около основания. Тогда

1) Площадь основания равна площади равностороннего треугольника:

Радиус описанной окружности

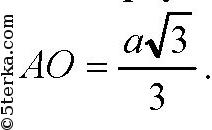
Тогда в ΔАО₁О:

Так что

2) Основание — квадрат с площадью S_осн=a². Радиус описанной окружности АО равен половине диагонали квадрата:

Далее, в ΔАОО₁:

Так что

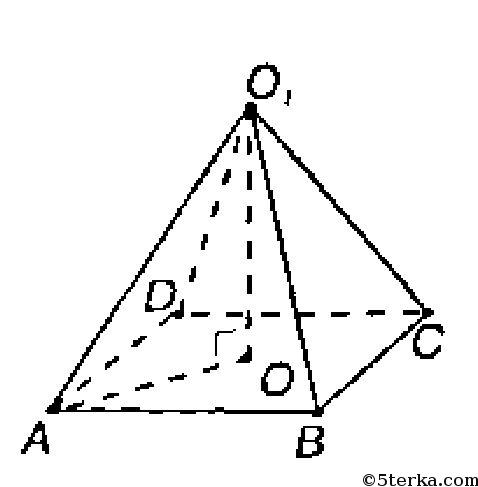
3)Площадь основания равна площади правильного шестиугольника, то есть площади шести равносторонних треугольников со стороной а.

Далее, Радиус описанной окружности равен стороне основания AO=a . Тогда в ΔАОО₁:

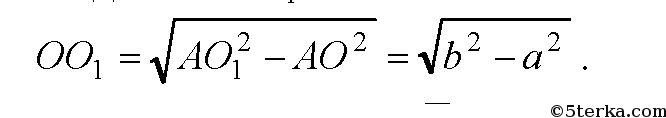
Ну и