35. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое ребро равно b. Найдите объем пирамиды.

Проведем высоту ОО₁ пирамиды. Поскольку все боковые ребра равны, то высота пирамиды проходит через центр описанной около основания окружности. Так что AO=R.

Далее в равнобедренных прямоугольных ΔAO₁B, ΔBO₁С, ΔAО₁С:

Так что в ΔAВС:

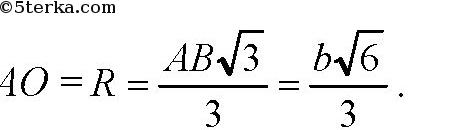
Далее площадь равностороннего ΔAВС равна

Затем в прямоугольном ΔAO₁O по теореме Пифагора получаем:

Тогда

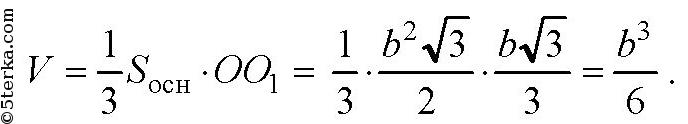
Ответ:

Источник:

Решебник по геометрии за 11 класс (А.В. Погорелов, 2001 год),
задача №35
к главе «§22. Объемы многогранников».

Все задачи

← 34. Сторона основания правильной шестиугольной пирамиды а, а двугранный угол при основании равен 45°. Найдите объем пирамиды.

36. Чему равен объем правильной треугольной пирамиды, у которой сторона основания а, а боковые ребра взаимно перпендикулярны? →

Комментарии