54. Найдите радиус шара, описанного около правильной n-угольной пирамиды, если сторона основания равна а, а боковое ребро наклонено к плоскости основания под углом α.

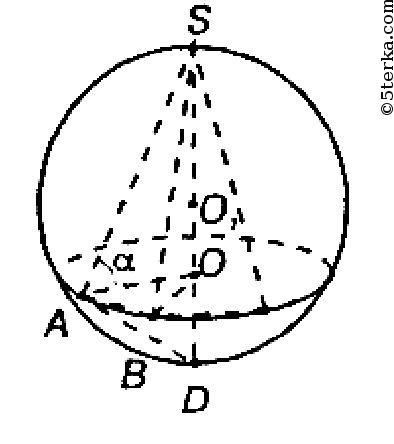
Проведем высоту SO правильной пирамиды. Тогда О — центр окружности, описанной около основания. Далее,

В прямоугольном ΔASO:

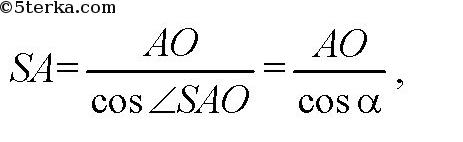
(радиус описанной окружности в правильном n-угольнике.

Тогда

Далее,

Рассмотрим осевое сечение шара, содержащее точку А . ∠SAD = 90° как вписанный угол, опирающийся на диаметр SD. Так как катет является средним пропорциональным между гипотенузой и проекцией катета на гипотенузу, то AS² =SD ⋅ SO (в ΔASD).

Так что

Тогда

— искомый радиус.