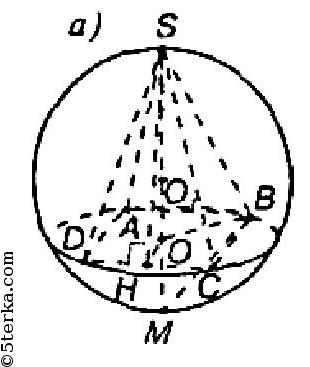
Проведем в пирамиде высоту SO и SH⊥DC. Тогда по теореме о трех перпендикулярах OH⊥DC. Тогда, так как ΔSDС равнобедренный, то SH является и медианой, и биссектрисой. Так что
Далее в ΔSHO:
Так что
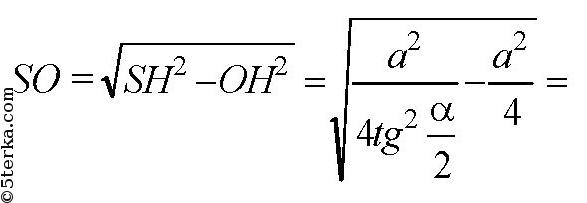
Далее, ∠SBM=90°, так как этот вписанный угол опирается на диаметр SM. Знаем, что катет является средним пропорциональным между гипотенузой и проекцией катета на гипотенузу, так что ВS2=SМ⋅SO, так что
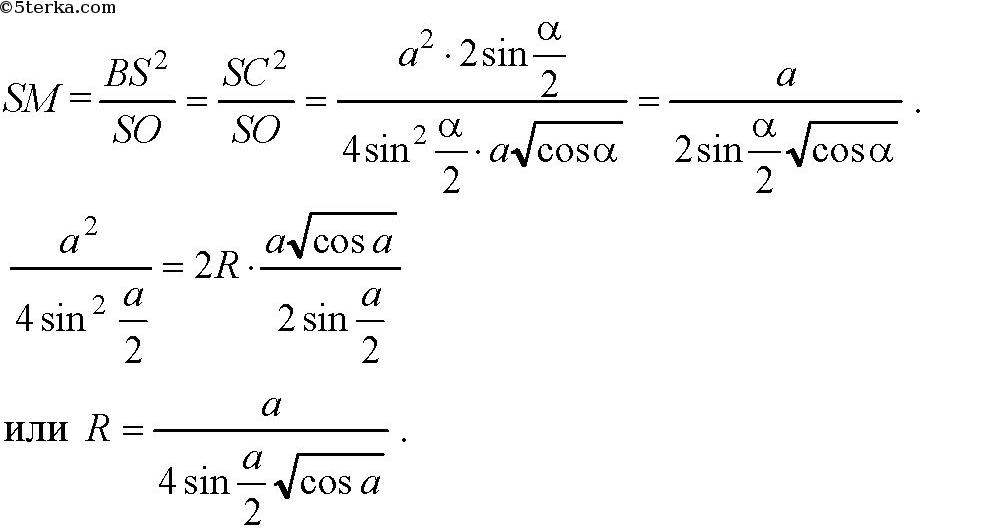
Так как радиус описанного шара
то
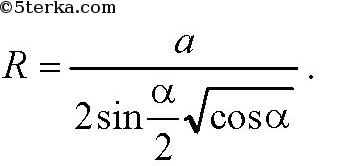
Далее, рассмотрим сечение пирамиды плоскостью SOH. OO2=EO2 — радиус вписанного шара. Имеем ΔSHО ~ ΔSO2E:
Так что
или
Так что
Источник:
Решебник
по
геометрии
за 11 класс (А.В. Погорелов, 2001 год),
задача №50
к главе «§21.Тела вращения».
Комментарии