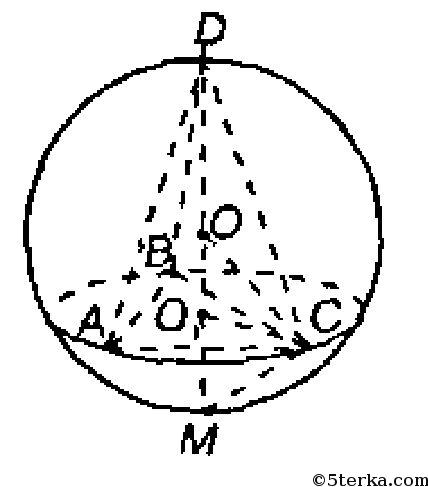
Пусть высота тетраэдра DО1 пересекает поверхность шара в некоторой точке М. Высота в правильной пирамиде проходит через центр окружности, описанной около основания. Так что O1С — радиус описанной около АВС окружности. ΔАВС равносторонний, так что

Рассмотрим осевое сечение шара, содержащее точку С. ΔDСM— прямоугольный, так как вписанный угол ∠DCM опирается на диаметр DM. Тогда катет DC — есть среднее геометрическое между
своей проекцией и гипотенузой. То есть
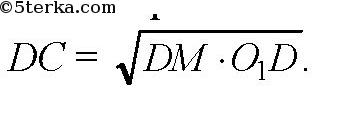
В ΔO1DC:

Тогда

А радиус шара

Источник:
 Решебник
по
геометрии
за 11 класс (А.В. Погорелов, 2001 год),
Решебник
по
геометрии
за 11 класс (А.В. Погорелов, 2001 год),
задача №49
к главе «§21.Тела вращения».
Комментарии