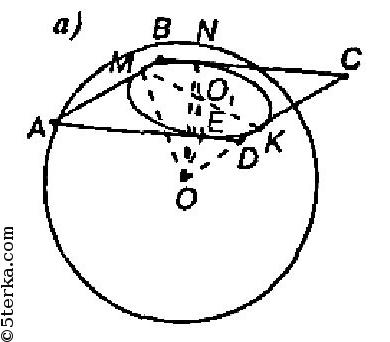
41. Диагонали ромба 15 см и 20 см. Шаровая поверхность касается всех его сторон. Радиус шара 10 см. Найдите расстояние от центра шара до плоскости ромба.

Проведем перпендикуляр ОО1 к плоскости ромба. Отрезки OM=ON=OK=OE= 10 см и перпендикулярны соответствующим сторонам ромба. Так что по теореме о трех перпендикулярах ОМ, O1N, О1К и О1Е перпендикулярны соответствующим сторонам ромба. Далее, ΔOO1M=ΔOO1N=ΔOO1К=ΔOO1E (по гипотенузе и катету). Так что O1M=O1N=O1K=O1E и значит, О1 — центр вписанной в ромб окружности.

В прямоугольном ΔAO1D (AC⊥BD):

Тогда

С другой стороны,

Тогда

Далее, в прямоугольном ΔОО1Е:

Ответ: 8 см.

Источник:

Домашняя работа по геометрии за 11 класс к учебнику «Геометрия. 10-11 класс» А.В. Погорелов Решебник по геометрии за 11 класс (А.В. Погорелов, 2001 год),
задача №41
к главе «§21.Тела вращения».

Все задачи

← 40. Стороны треугольника 13см, 14см и 15см. Найдите расстояние от плоскости треугольника до центра шара, касающегося всех сторон треугольника. Радиус шара 5см.
42. Через касательную к поверхности шара проведены две взаимно перпендикулярные плоскости, пересекающие шар по кругам радиусов r1 и r2 Найдите радиус шара R. →
Комментарии