40. Стороны треугольника 13см, 14см и 15см. Найдите расстояние от плоскости треугольника до центра шара, касающегося всех сторон треугольника. Радиус шара 5см.

Проведем OO1 перпендикулярно плоскости ΔMNK. Так как стороны ΔMNK касаются шара, то OA, OВ и ОС перпендикулярны сторонам ΔMNK. Тогда по теореме о трех перпендикулярах O1A, O1B и О1С тоже перпендикулярны к соответствующим сторонам ΔMNK.

Далее, так как ΔАОО1=ΔВОО1=ΔСОО1 (по катету и гипотенузе), то: O1A=O1B=O1C. Так что О1 — центр вписанной окружности в ΔMNK. Площадь ΔMNK равна:

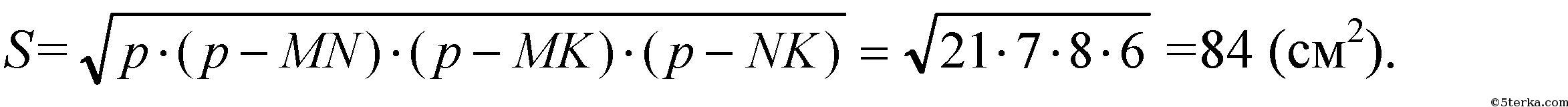
Но S=pr, так что

Далее, в прямоугольном Delta;AОО1:

Ответ: 3 см.

Источник:

Домашняя работа по геометрии за 11 класс к учебнику «Геометрия. 10-11 класс» А.В. Погорелов Решебник по геометрии за 11 класс (А.В. Погорелов, 2001 год),
задача №40
к главе «§21.Тела вращения».

Все задачи

← 39. Шар радиуса R касается всех сторон правильного треугольника со стороной а. Найдите расстояние от центра шара до плоскости треугольника
41. Диагонали ромба 15 см и 20 см. Шаровая поверхность касается всех его сторон. Радиус шара 10 см. Найдите расстояние от центра шара до плоскости ромба. →
Комментарии