36. Радиус шара 7 см. На его поверхности даны две равные окружности, имеющие общую хорду длиной 2 см. Найдите радиусы окружностей, зная, что их плоскости перпендикулярны.

Из центра шара О проведем перпендикуляры ОО₁ и ОВ к плоскостям соответствующих окружностей. Из точек О₁ и В проведем перпендикуляры О₁В₁ и ВВ₁ к общей хорде АС. Тогда

Далее, в прямоугольном ΔO₁AB₁, если O₁A=R и C₁B=a, то получим

В прямоугольном ΔBCB₁ обозначим

тогда

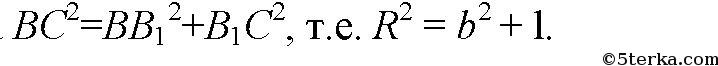
Так что а=b, то есть О₁В₁=ВВ₁

Тогда OO₁BB₁ — квадрат и его диагональ

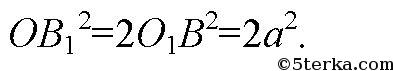
Далее, в прямоугольном ΔOAB₁ OA=7 см, тогда

то есть

Далее

так что

Ответ: 5 см.

Источник:

Решебник по геометрии за 11 класс (А.В. Погорелов, 2001 год),
задача №36
к главе «§21.Тела вращения».

Все задачи

← 35. Диаметр шара 25 см. На его поверхности даны точка А и окружность, все точки, которой удалены (по прямой) от А на 15 см. Найдите радиус этой окружности.

37. Дан шар радиуса R. Через одну точку его поверхности проведены две плоскости: первая — касательная к шару, вторая — под углом 30° к первой. Найдите площадь сечения. →

Комментарии