34. На поверхности шара даны три точки. Прямолинейные расстояния между ними 6 см, 8 см, 10 см. Радиус шара 13 см. Найдите расстояние от центра до плоскости, проходящей через эти точки.

Проведем OO₁ перпендикулярно плоскости ΔАВС. Тогда прямоугольные треугольники АO₁O, BO₁O, СО₁О равны по катету и гипотенузе (так как AO=BO=CO — радиус шара и ОО₁— общий катет). Так что О₁—центр окружности, описанной около треугольника АВС (О₁А=О₁В=О₁С).

Далее, заметим, что 6² + 8² = 10², так что ΔАВС прямоугольный с гипотенузой АС. Поэтому О₁ — середина АС, так что

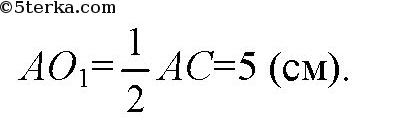
Далее, в прямоугольном ΔAOO₁:

Ответ: 12 см.

Источник:

Решебник по геометрии за 11 класс (А.В. Погорелов, 2001 год),
задача №34
к главе «§21.Тела вращения».

Все задачи

← 33. Город N находится на 60° северной широты. Какой путь совершает этот пункт в течение 1ч. вследствие вращения Земли вокруг своей оси?

35. Диаметр шара 25 см. На его поверхности даны точка А и окружность, все точки, которой удалены (по прямой) от А на 15 см. Найдите радиус этой окружности. →

Комментарии