28. Полушар и вписанный в него конус имеют общее основание и общую высоту. Через середину высоты проведена плоскость, параллельная основанию. Докажите, что площадь сечения, заключенного между боковой поверхностью конуса и поверхностью полушара, равна поло

Рассмотрим осевое сечение конуса СОА.

Тогда ΔСО₁А₁ ~ ΔСОА, так что

так что

В прямоугольном ΔOO₁B по теореме Пифагора:

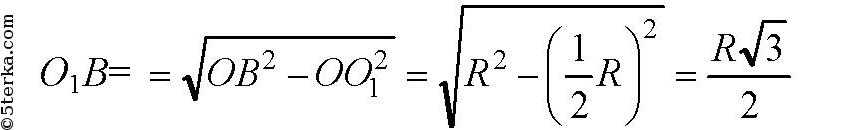
Искомая площадь сечения равна разности площадей кругов с радиусом О₁В и О₁А:

А площадь основания S_O = πOA² = πR², так что площадь сечения равна половине площади основания, что и требовалось доказать.