20. Радиусы оснований усеченного конуса R и r, образующая наклонена к основанию под углом 45°. Найдите высоту Н.

Рассмотрим осевое сечение усеченного конуса. Им является ABCD — равнобокая трапеция с основаниями

BС = 2 ⋅ ВО₁ = 2r и AD = 2 ⋅ AO = 2R. Далее, проведем BM⊥AD и CK⊥AD. Тогда

ВСКМ — прямоугольник и ВС = МК, ВМ = СК. ΔАВМ = ΔDCK. Так что

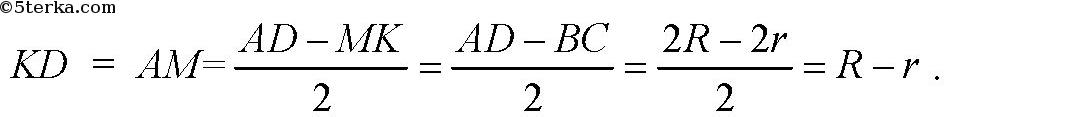
Далее, ΔАМВ равнобедренный, так как ∠А = ∠АВМ = 45°. Так что H=BM=AM=R-r.

Ответ: R-r.

Источник:

Решебник по геометрии за 11 класс (А.В. Погорелов, 2001 год),
задача №20
к главе «§21.Тела вращения».

Комментарии