1183 Даны две параллельные прямые b и с и точка А, не лежащая ни на одной из них них. Постройте равносторонний треугольник ABC так, чтобы вершины В и С лежали соответственно на прямых b и c. Сколько решений имеет задача?

1183 Даны две параллельные прямые b и с и точка А, не лежащая ни на одной из них них. Постройте равносторонний треугольник ABC так, чтобы вершины В и С лежали соответственно на прямых b и c. Сколько решений имеет задача?

Решение из учебника

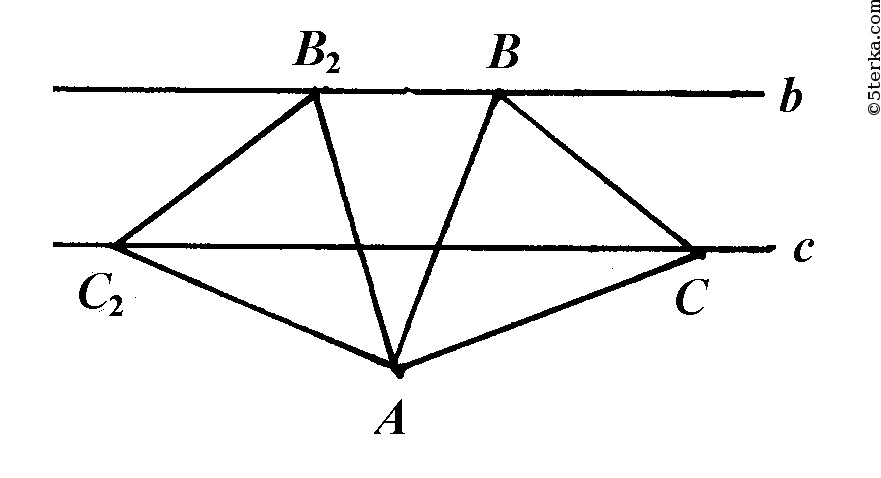
Допустим, что задача решена и искомый треугольник ABC построен (рис. 334, а). При повороте плоскости вокруг точки А на 60° по часовой стрелке вер-шина В отображается в вершину С, поэтому прямая b отображается на прямую b₁, проходящую через точку С. Прямую b₁ легко построить, не пользуясь точками В и С (см. задачу 1171). Построив прямую b₁ находим точку С, в которой прямая b₁ пересекается с прямой с. Затем, построив окружность с центром А радиуса АС, находим точку В. На рисунке 334, а выполнено построение.

Задача имеет два решения, одно из которых получается при повороте плоскости вокруг точки А на 60° по часовой стрелке (ΔАВС на рисунке 334, а), а другое — при повороте плоскости на угол 60° против часовой стрелки (ΔАВ'С' на рисунке 334, б).

Решение №2

Где бы точка A не лежала, существует два решения задачи.