885 Через каждую вершину треугольника ABC проведена прямая, перпендикулярная к биссектрисе угла треугольника при этой вершине. Проведенные прямые, пересекаясь, образуют новый треугольник. Докажите, что вершины этого треугольника лежат на прямых, содержащи

885 Через каждую вершину треугольника ABC проведена прямая, перпендикулярная к биссектрисе угла треугольника при этой вершине. Проведенные прямые, пересекаясь, образуют новый треугольник. Докажите, что вершины этого треугольника лежат на прямых, содержащих биссектрисы треугольника ABC.

Решение.

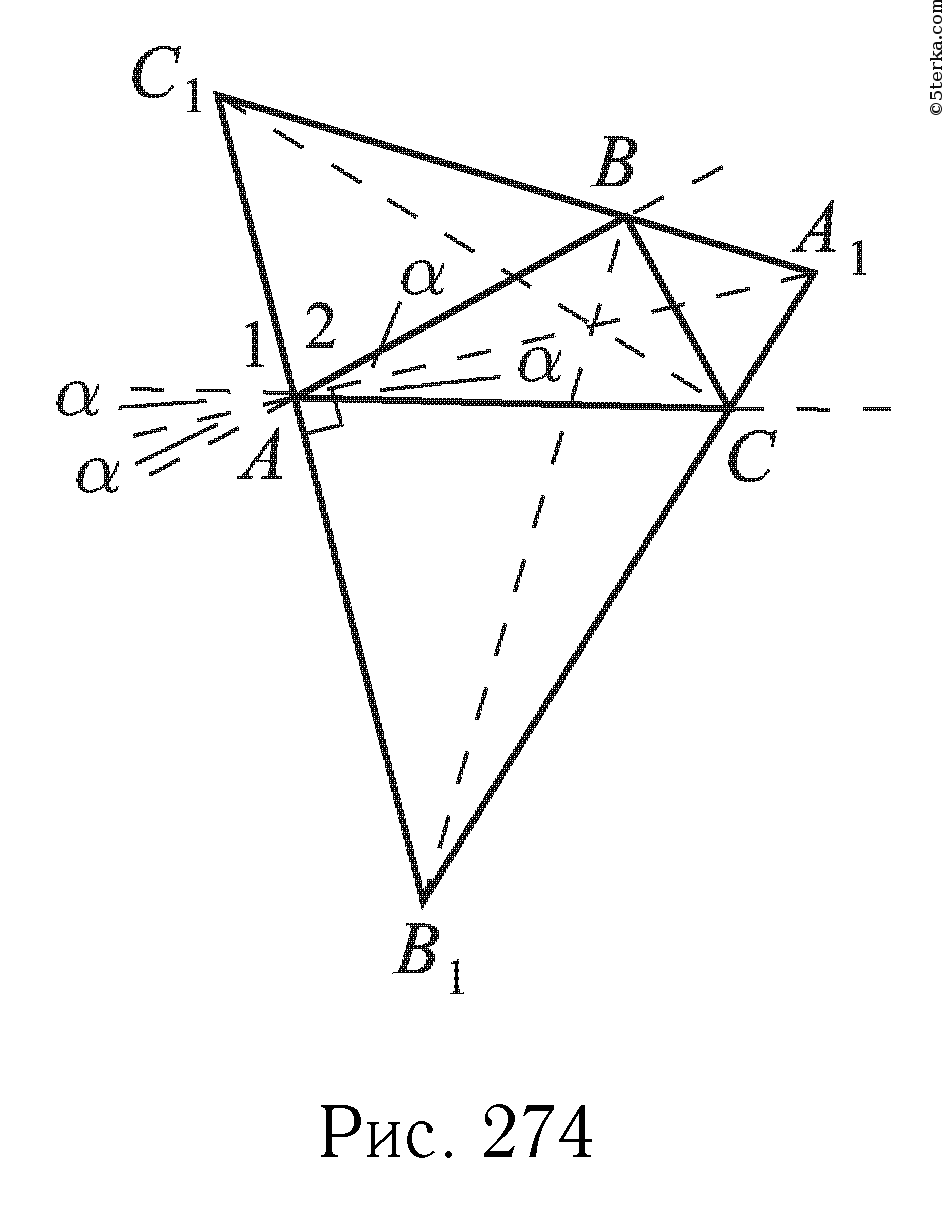
Поскольку точка А₁ лежит на биссектрисе внешнего угла В треугольника ABC, то она равноудалена от прямых АВ и ВС. По аналогичной причине она равноудалена от прямых АС и ВС. Следовательно,

она равноудалена от прямых АВ и АС, а значит, лежит на биссектрисе угла ВАС. Иными словами, она лежит на прямой, содержащей биссектрису треугольника ABC, проведенную из вершины А.

Источник:

Решебник по геометрии за 8 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2005 год),
задача №885
к главе «Глава VIII. Окружность. Задачи повышенной трудности».

Все задачи

← 884 Внутри угла ABC равностороннего треугольника ABC взята точка М так, что ∠BMC=30°, ∠BMA= 17°. Найдите углы ВАМ и ВСМ.

886 Пусть Н — точка пересечения прямых, содержащих высоты треугольника ABC, а А', В', С' — точки, симметричные точке Н относительно прямых ВС, СА, АВ. Докажите, что точки А', В', С' лежат на окружности, описанной около треугольника ABC. →

Комментарии