828 Докажите, что если треугольник имеет: а) ось симметрии, то он равнобедренный; б) более чем одну ось симметрии, то он равносторонний.

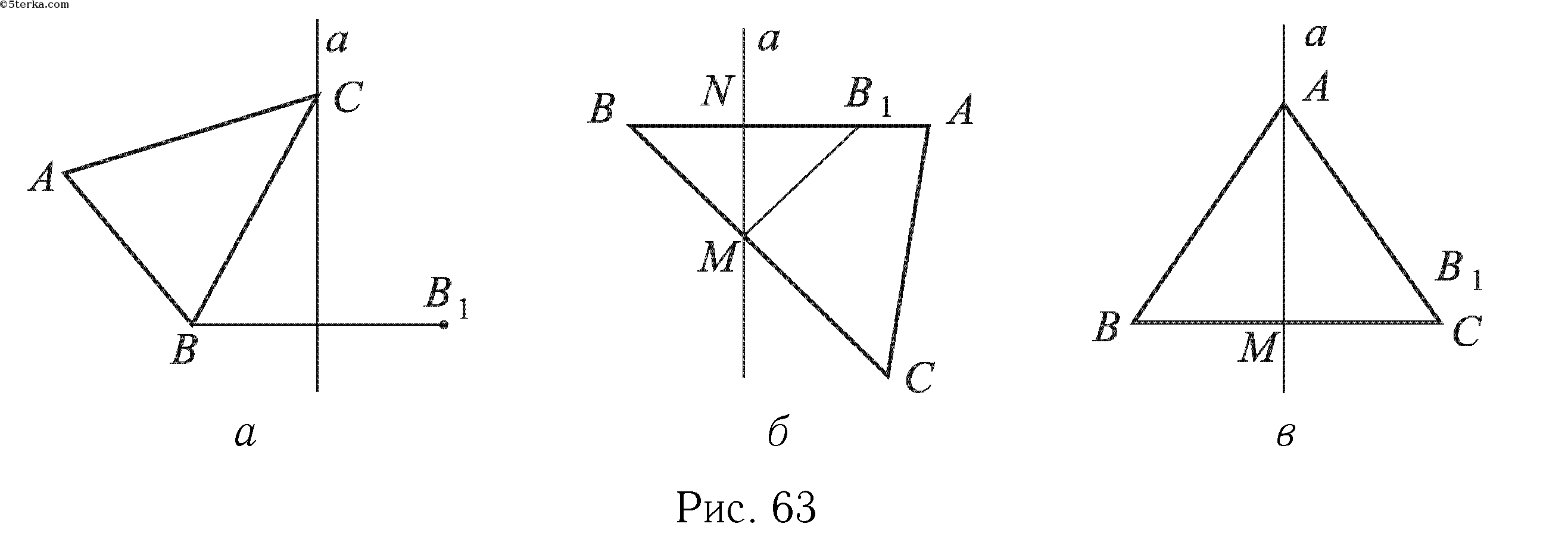
Решение. а) Пусть прямая а — ось симметрии треугольника ABC. Тогда прямая а имеет по крайней мере одну общую точку с треугольником (объясните, почему). Более того, прямая а пересекает хотя бы одну из сторон треугольника, так как в противном случае точка, симметричная вершине треугольника, не лежащей на прямой а, не может принадлежать треугольнику (рис. 63, а).