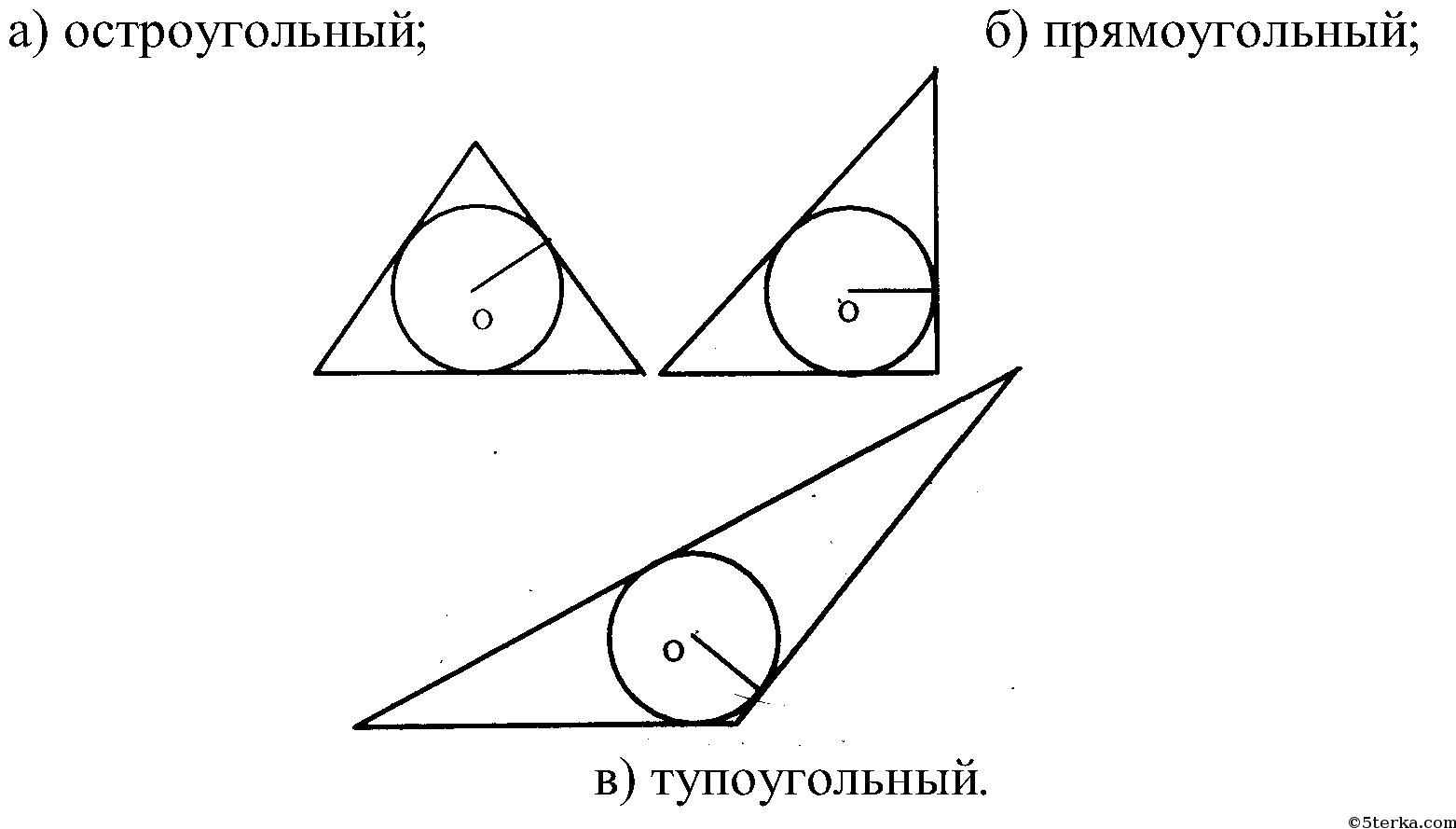
Решение. Чтобы вписать окружность в данный треугольник, нужно построить биссектрисы двух его углов и найти точку их пересечения — центр вписанной окружности. Затем из этой точки следует провести перпендикуляр к какой-нибудь стороне. Окружность с найденным центром, проходящая через основание этого перпендикуляра, — искомая вписанная окружность.
Источник:
 Решебник
по
геометрии
за 8 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2005 год),
Решебник
по
геометрии
за 8 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2005 год),
задача №701
к главе «Глава VIII. Окружность. §4. Вписанная и описанная окружности».
Комментарии