700 Докажите, что в любой ромб можно вписать окружность.

Суммы противоположных сторон ромба равны, следовательно, в любой ромб можно вписать окружность.

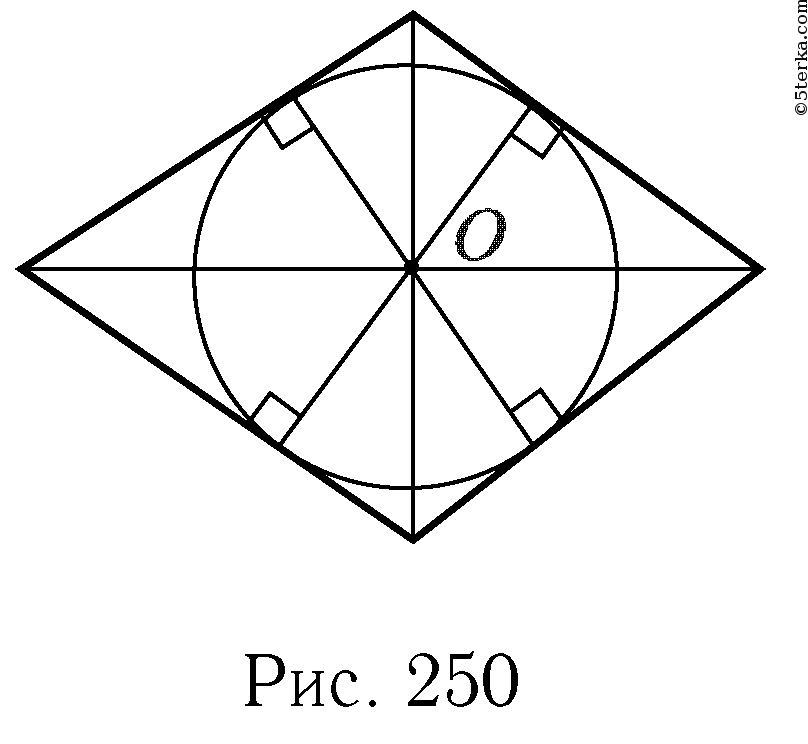
Решение #2. Диагонали ромба взаимно перпендикулярны и делятся точкой пересечения пополам. Поэтому диагонали ромба разделяют его на четыре прямоугольных треугольника, равных друг другу по двум катетам. Следовательно, высоты этих треугольников, проведенные из вершины О прямых углов, также равны. Иными словами, если провести окружность с центром О, проходящую через основание одной из этих высот, то она пройдет и через основания трех других высот (рис. 250).

Стороны ромба касаются этой окружности, так как они соответственно перпендикулярны к ее радиусам.