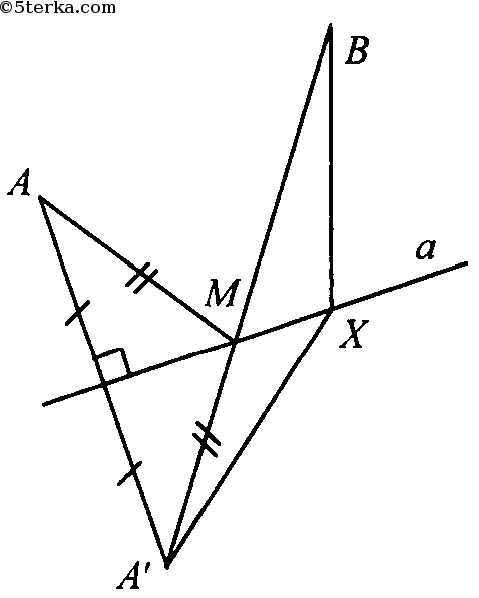
Пусть М - пересечение А'В и пр. а. М- искомая точка, поскольку выполняется неравенство треугольника:
АМ+ МВ = А'М+ MB (т.к. ΔАА'М- равнобедренный) = А'В < АХ + ХВ.
Источник:
 Решебник
по
геометрии
за 7 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2012 год),
Решебник
по
геометрии
за 7 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2012 год),
задача №355
к главе «Задачи на построение».
Комментарии