814. Все высоты тетраэдра пересекаются в точке Н. Докажите, что точка Н, центр О описанной сферы и точка G пересечения отрезков, соединяющих вершины с точками пересечения медиан противоположных граней тетраэдра, лежат на одной прямой (прямая Эйлера), причем точки О и H симметричны относительно точки G.

Лемма 1. (Геометрия 7—9, стр. 141, Геометрия 10— 11, стр. 94.). Все медианы в треугольнике A₁A₂A₃ пересекаются в одной точке М, называемой центроидом треугольника, где для любой точки О

(1)

и M делит каждую медиану в соотношении 2:1.

Если С₁ - середина A₂A₃„ то (Геометрия 7—9, стр. 199)

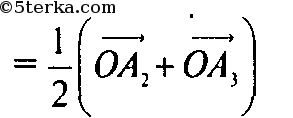
Точка M, определяемая равенством (1), лежит на медиане А₁С₁ и делит её в соотношении 2 : 1. Действительно:

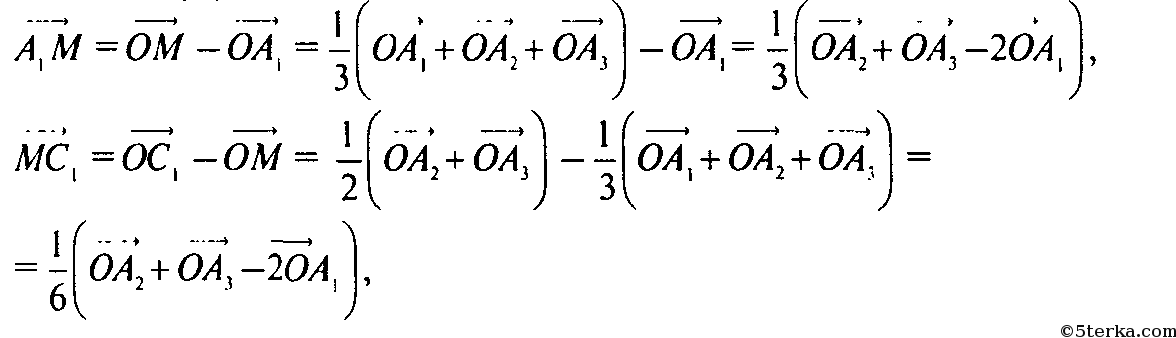
откуда

и

Для остальных

медиан доказательство аналогично.

Лемма 2. Все прямые, соединяющие вершины тетраэдра A₁A₂A₃A₄ с центроидами противоположных граней, пересекаются в одной точке G (называемой центроидом тетраэдра), где

Если М₄ - центроид грани A₁A₂A₃, то

следовательно,

откуда

причем

Для остальных прямых доказательство аналогично.

По условию все высоты тетраэдра A₁A₂A₃A₄ пересекаются в точке H. Пусть G - центроид тетраэдра; докажем, что точка С, для кото-

рой

является центром описанной около тетраэдра сферы, то есть, что

или

Согласно лемме 2:

(2)

Аналогично

(3)

Так как

то

Аналогично равны друг другу все произведения вида

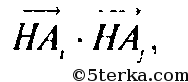
где

После раскрытия скобок в (2) и (3) все удвоенные произведения окажутся равными между собой, так что

Аналогичны верны и остальные равенства (1). Так как

то точки H, С и G лежат на одной прямой.