813. Шар образован вращением полукруга вокруг прямой, содержащей диаметр. При этом поверхность, образованная вращением некоторой хорды, один конец которой совпадает с концом данного диаметра, разбивает шар на две равные по объему части. Найдите косинус угла между этой хордой и диаметром.
Пусть AB- диаметр полукруга, R — его радиус, О — его центр, OK ⊥ АС, CD ⊥ АВ. Объем тела, полученного при вращении фигуры ANC, равен разности объемов шарового сегмента, полученного при вращении ANCD, и конуса, полученного при вращении ADC: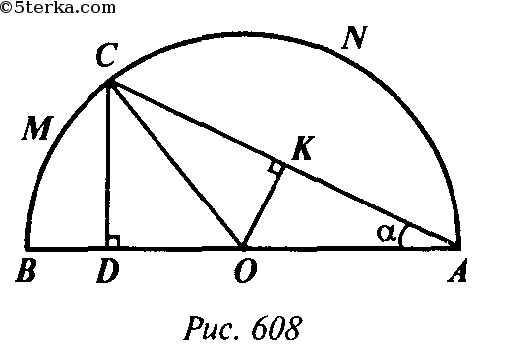
Но
следовательно,
По условию VANC равен половине объема шара:
Источник:
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №813
к главе «Задачи повышенной трудности».
Комментарии