812. Правильная четырехугольная пирамида, у которой сторона основания равна а, а плоский угол при вершине равен а, вращается вокруг прямой, проходящей через вершину параллельно стороне основания. Найдите объем полученного тела вращения.

При повороте пирамиды SABCD вокруг прямой p, параллельной АВ, отрезки A0A, SM, В0В, перпендикулярные р, займут соответственно положения A0A1, SM1, B0B1 в плоскости

SA2B2.

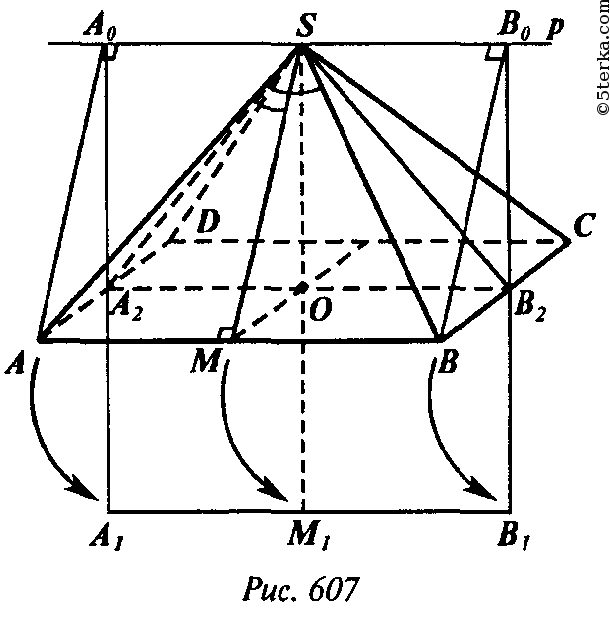
Поэтому тело, полученное при ее вращении, совпадает с телом, полученным при вращении многоугольника A1A2SB2B1. Его объем равен разности между объемом цилиндра, полученного при вращении прямоугольника A1B1B0A0, и объемами конусов, полученных при вращении равных треугольников A2A1S и B2B0S.

Из ΔASM:

Из ΔOSM:

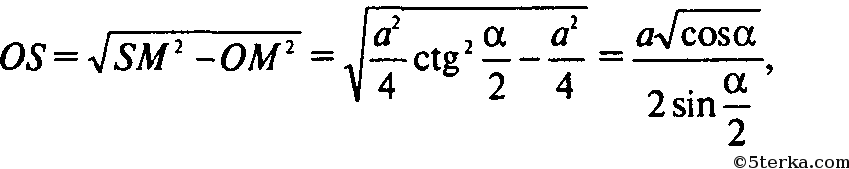
но

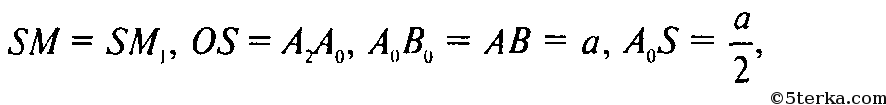
поэтому объем тела

вращения равен

Источник:

Решебник по геометрии за 10 класс к учебнику Геометрия. 10-11 класс Л.С.Атанасян Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №812
к главе «Задачи повышенной трудности».

Все задачи

← 811. В конус вписан шар. Докажите, что отношение объемов конуса и шара равно отношению площадей полной поверхности конуса и сферы, являющейся границей шара.
813. Шар образован вращением полукруга вокруг прямой, содержащей диаметр. При этом поверхность, образованная вращением некоторой хорды, один конец которой совпадает с концом данного диаметра, разбивает шар на две равные по объему части. Найдите косинус уг →
Комментарии