801. На плоскости лежат три шара радиуса R, попарно касающиеся друг друга. Основание конуса лежит в указанной плоскости, а данные шары касаются его извне. Высота конуса равна λR. Найдите радиус его основания.

Если A₁,A₂,A₃ — точки касания шаров с плоскостью и О — центр основания конуса, то A₁A₂ = A₁А₃ = A₂А₃ = 2R и О — центр окружности, описанной около треугольника A₁A₂A₃

Следовательно,

Пусть треугольник ASB — осевое сечение конуса, OA = r — радиус его основания, ∠OAS— α, О₁ — центр одного из шаров, С, — точка касания этого шара и конуса. Тогда в четырехугольнике A₁AC₁O₁:

следовательно, ∠A₁O₁C₁ = α, а так как

то

Из ΔAOS:

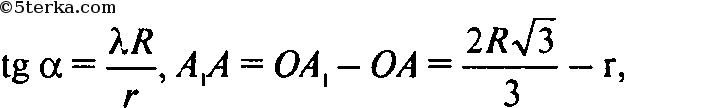
из ΔO₁A₁A:

Подставляя эти значения в формулу

получим после упрощений:

При λ < 2 только этот корень положителен.

При λ > 2 оба корня положительны, но больший корень r₂ оказывается большим, чем

то есть радиус круга, описанного

около

находятся внутри основания конуса и касание является не внешним, а внутренним;