792. Докажите, что высоты тетраэдра пересекаются в одной точке тогда и только тогда, когда противоположные ребра тетраэдра перпендикулярны.

Пусть высоты АА₁, ВВ₁, СС₁, DD₁ тетраэдра ABCD пересекаются в точке H; α — плоскость АВН,

Т. к.

и

то

аналогично

Т. к.

то

но

следовательно,

Аналогично доказывается, что

Обратно, пусть

α - плоскость АВА₁.

Так как

а поскольку и по ус

ловию

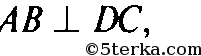
то

Так как

но вместе с

тем

Поскольку

и

то

то

есть ВВ₀ совпадает с высотой ВВ₁ тетраэдра.

Таким образом, высоты АA₁ и ВВ₁ тетраэдра пересекаются в точке H; аналогично и остальные высоты тетраэдра попарно пересекаются. Их точки пересечения совпадают, так как в противном случае все высоты тетраэдра лежали бы в одной плоскости.