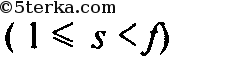
поверхность Ps с числом
граней fs, ребер ks и вершин es.
Докажем индукцией по числу граней, равному
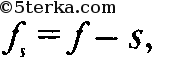
что
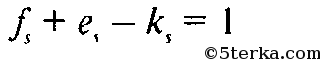
(1)
При
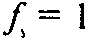
(то есть s = f— 1) равенство (1) верно, так как тогда
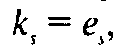
откуда
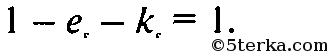
Пусть (1) верно для
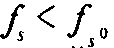
, докажем (1) для
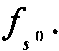
Разрежем
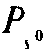
по ломаной, соединяющей две вершины, лежащие
на краю, образованной ребрами и не пересекающей себя. Получим поверхности
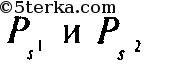
соответственно с
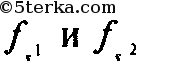
гранями,
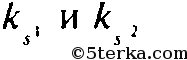
ребрами,
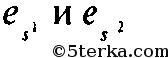
вершинами. Так как
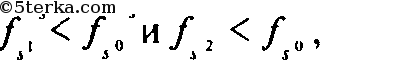
то
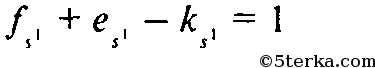
(2)
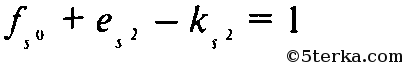
(3)
Пусть n — число ребер разреза; тогда число его вершин n + 1. Если сосчитать число ребер или вершин на
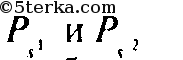
и результаты сложить, то каждое ребро или вершина разреза будут сосчитаны дважды; поэтому
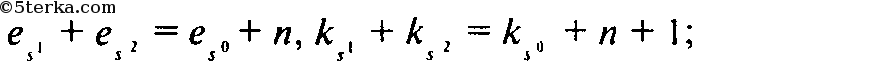
кроме
того,
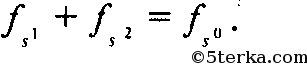
Тогда, складывая (2) и (3), получим
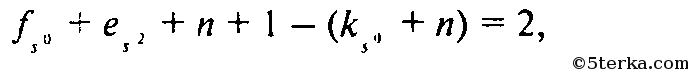
то есть
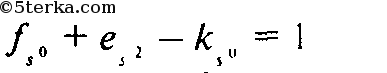
и (1)
доказано для
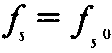
Тем самым (1) верно для любого fs.
В частности, при
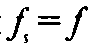
(то есть при s=1) имеем
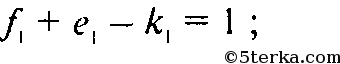
так как
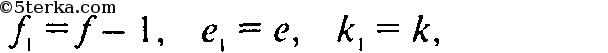
то
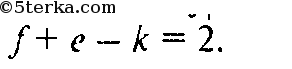
 Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №784
к главе «Задачи повышенной трудности».