766. Докажите, что сумма квадратов двух противоположных ребер тетраэдра вдвое больше суммы квадратов отрезков, соединяющих соответственно середины остальных противоположных ребер.

В обозначениях рисунка к задаче 765 по свойству средней линии MN || AD || LK, аналогично ML || NK и MNKL — параллелограмм.

Тогда

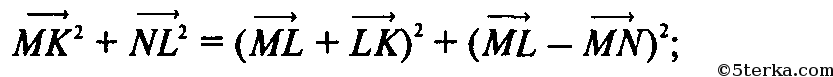
т. к.

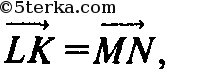
то

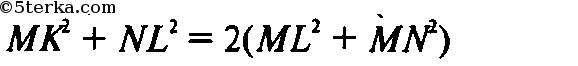
- сумма квадратов диагоналей па-

раллелограмма равна сумме квадратов всех его сторон. Если

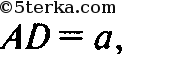
и

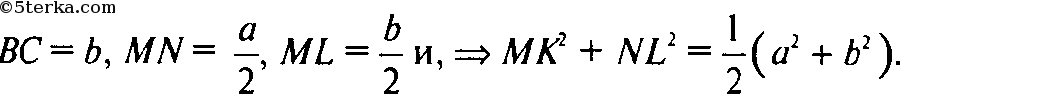
Источник:

Решебник по геометрии за 10 класс к учебнику Геометрия. 10-11 класс Л.С.Атанасян Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №766
к главе «Задачи повышенной трудности».

Все задачи

← 765. Дан тетраэдр, все ребра которого равны. Докажите, что периметры фигур, которые получаются при пересечении этого тетраэдра плоскостями, параллельными двум противоположным ребрам, равны.
767. Известно, что из любого равностороннего треугольника можно склеить тетраэдр, перегибая его по трем средним линиям и склеивая соответствующие части его сторон (см. рис. 88). Какому условию должны удовлетворять углы произвольного треугольника, чтобы из →
Комментарии