764. Даны две скрещивающиеся прямые, угол между которыми равен 90°. Найдите множество середин всех отрезков данной длины d, концы которых лежат на этих прямых.

Пусть a, b — данные прямые, АВ — данный отрезок, М — его середина (рис. 566),

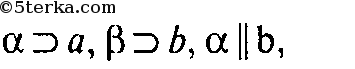
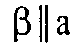
(учебник, стр. 16). AB = d, h — расстояние между α и β, μ — плоскость, равноудаленная от α и β,

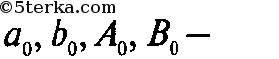
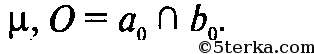
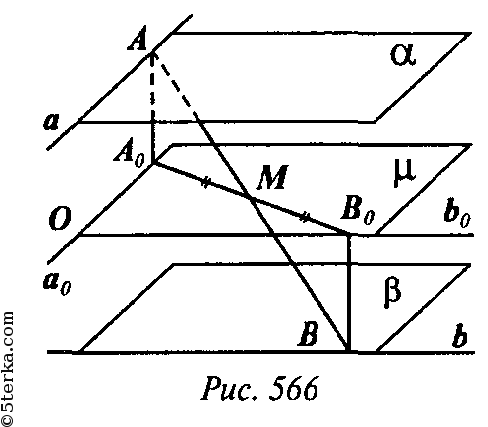
Тогда

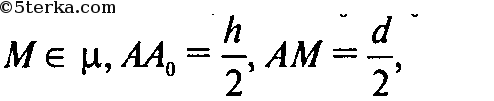
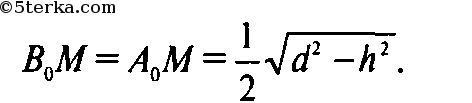
В

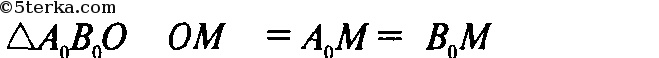
как радиусы окружностей с диаметром А₀B₀. Следовательно, М лежит на окружности в

плоскости μ с центром О и радиусом

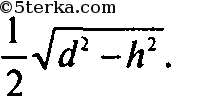
Проводя рассуждения в обратном порядке, убедимся, что любая точка этой окружности — середина отрезка длины d с концами на a и b.