759. В шар вписана пирамида, основанием которой является прямоугольный треугольник с гипотенузой, равной 2 см. Найдите площадь поверхности и объем шара, если каждое боковое ребро пирамиды составляет с основанием угол α.

Плоскость треугольника АВС, лежащего в основании пирамиды, пересечет шар по окружности, и треугольник АВС будет вписан в эту окружность. Пусть

АВ — гипотенуза, следовательно, ∠АСВ=90°, тогда, он опирается на диаметр, которым является гипотенуза АВ.

Построим высоту пирамиды МО. Построим отрезки ОА, ОВ, ОС; эти три отрезка являются проекциями соответствующих наклонных боковых ребер пирамиды.

В треугольниках МОА, МОВ, МОС МО — общий катет, ∠МАО=

=∠МВО=∠МСО=α — по условию, тогда, ΔМОА=ΔМОВ=ΔМОС, откуда ОА=ОВ=ОС, то есть точка О — равноудалена от вершин основания и поэтому является центром описанной около основания окружности.

Таким образом, МО — высота пирамиды, МО лежит в плоскости АМВ, тогда, плоскость АМВ перпендикулярна плоскости АВС

Из теоремы синусов следует, что:

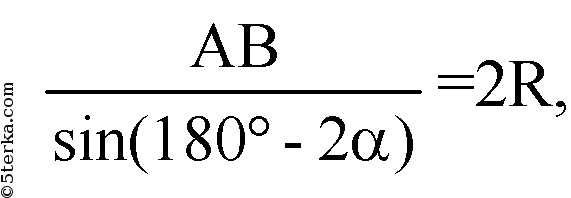
R — радиус шара.

Площадь поверхности шара:

Вычислим объем шара: