760. В шар вписана пирамида, основанием которой является прямоугольник с диагональю 10 см. Каждое боковое ребро пирамиды составляет с основанием угол р. Найдите площадь поверхности и объем шара.

Построим высоту пирамиды MF; построим отрезки FA, FB, FC, FD.

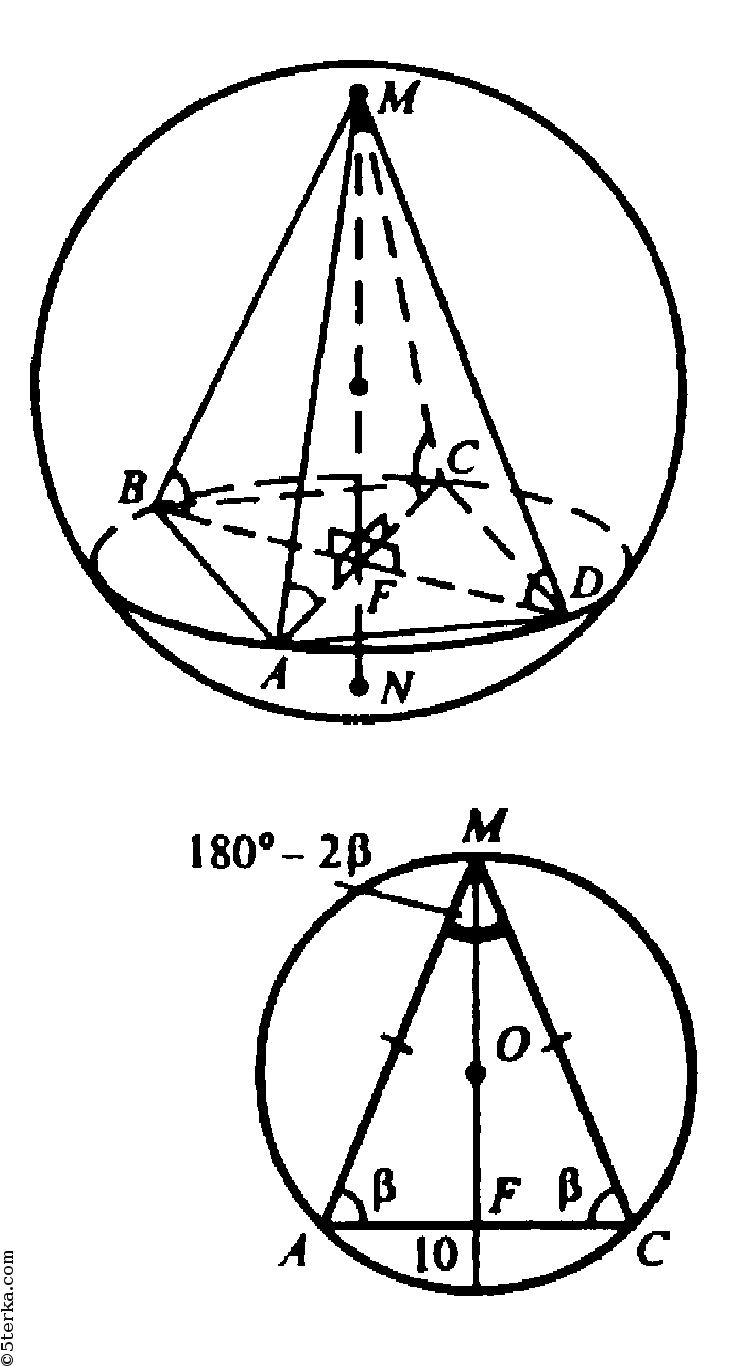
т.к. они прямоугольные, MF — общий ка-

тет,

— по условию.

Следовательно, FA=FB=FC=FD, тогда точка F равноудалена от вершин основания, значит, является центром описанной около основания окружности.

Рассмотрим сечение пирамиды и шара плоскостью АМС. Точка О — центр шара, O∈MF.

Из теоремы синусов в треугольнике АМС:

где R — радиус шара.

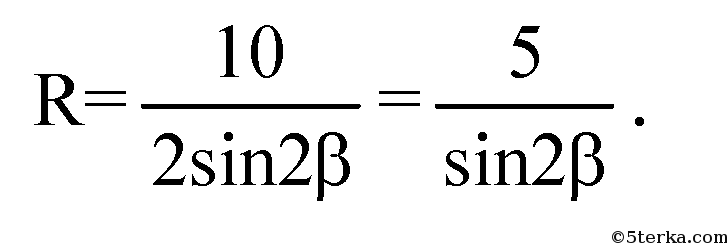
Площадь поверхности шара:

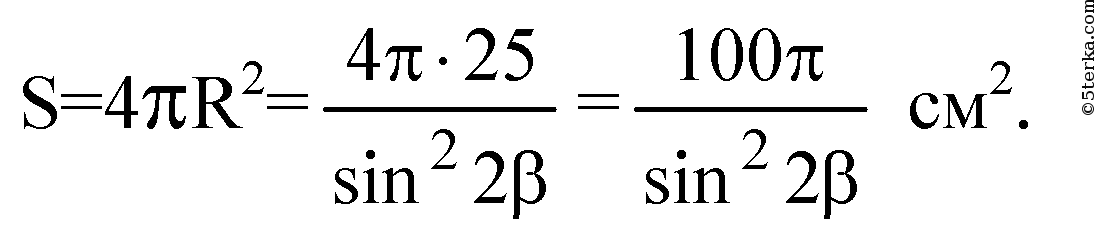
Объем шара: