Н1,H2 — центры оснований. ABCD — сечение, которое является равнобедренной трапецией.
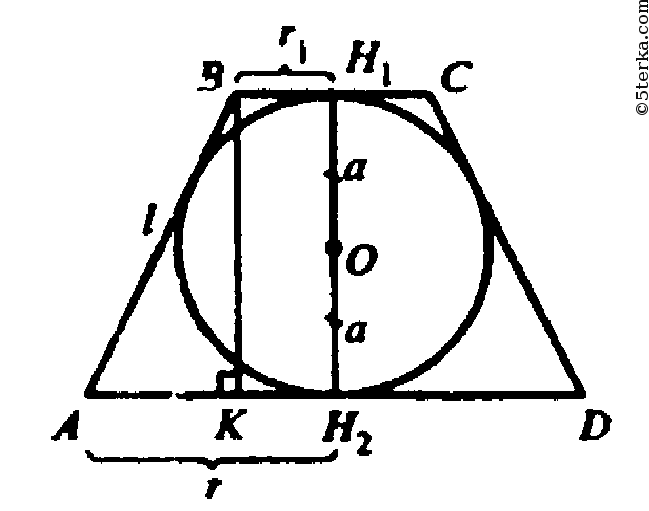
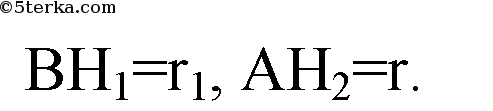
Обозначим радиус вписанного шара а.
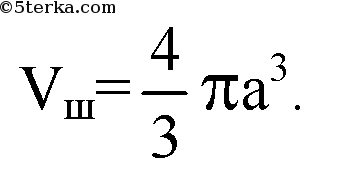
Высота конуса есть диаметр шара, Н1Н2=2а.
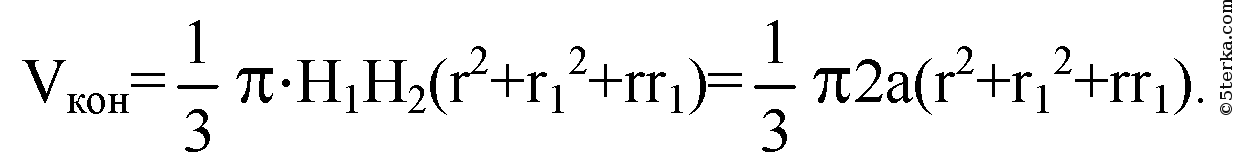
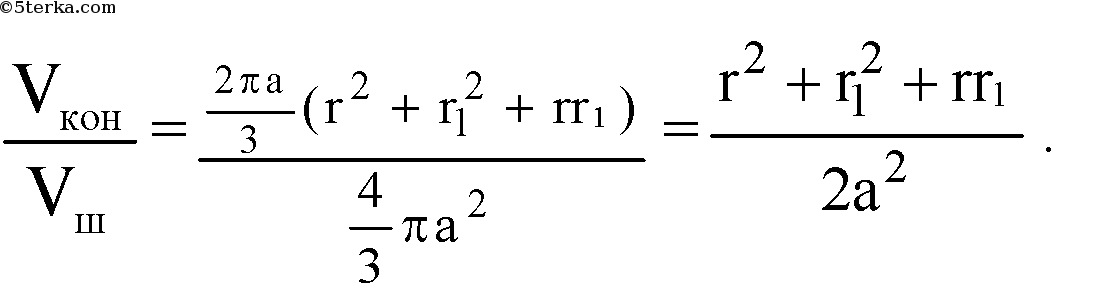
В описанном 4-угольнике суммы противоположных сторон равны. ВС+AD=AB+CD=2AB.
Обозначим АВ=l, следовательно 2r1+2r=2l, l=r1+r.
Построим ВК перпендикулярно AD. АК=г-r1, ВК=Н1Н2=2а.
Из прямоугольного треугольника АВК:
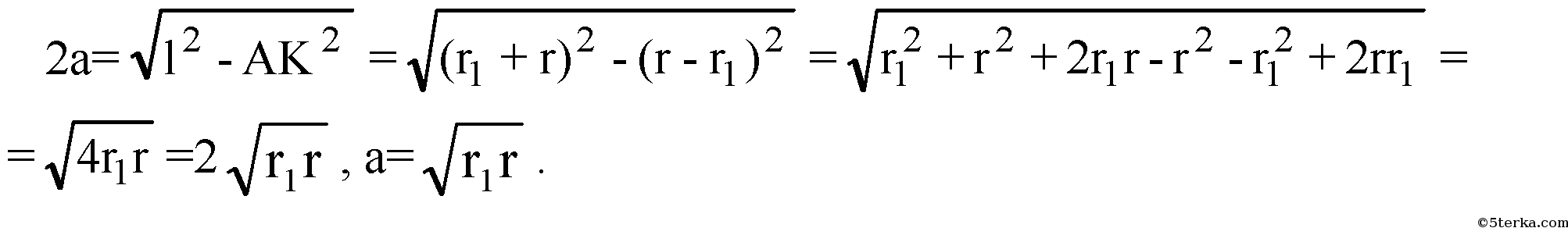
Подставляя выражение для а в формулу (1), получаем:
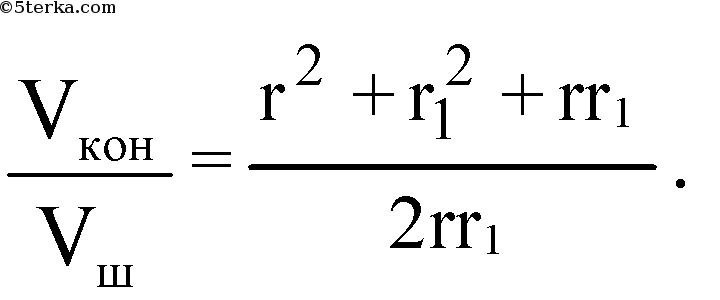
Источник:
 Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №753
к главе «Разные задачи на многогранники, цилиндр, конус и шар».
Комментарии