738. Высота правильной треугольной пирамиды равна h, а двугранный угол, ребром которого является боковое ребро пирамиды, равен 2φ. Найдите объем пирамиды.

Имеем DO — высота пирамиды, плоскость DOC⊥ плоскости АВС. Проведем ОМ ⊥ DC, через точку О проведем KL параллельно AB, отрезки ML и МК. KL перпендикулярно плоскости DOC, значит, KL⊥DC.

OM⊥DC — по построению. Плоскость KLM⊥DC и поэтому LM⊥DC и КМ⊥DC.

Тогда, ∠KML=2 φ, ΔKOM=ΔLOM, значит ∠KMO=∠LMO= φ .

Пусть ∠ODM= α, следовательно, из прямоугольного ΔODM: ОМ=h sinα .

Примем KO=OL=y. Из прямоугольного ΔLOM:

Рассмотрим треугольник АВС. В нем ОС — радиус описанной окружности, OС=R, а OF — радиус вписанной окружности. OF=r. Обозначим сторону основания х, следовательно,

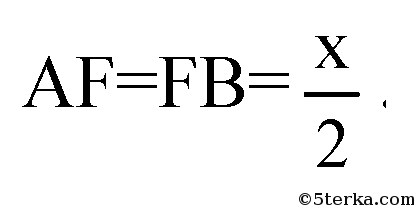
Из подобия треугольников FCB и OLC имеем:

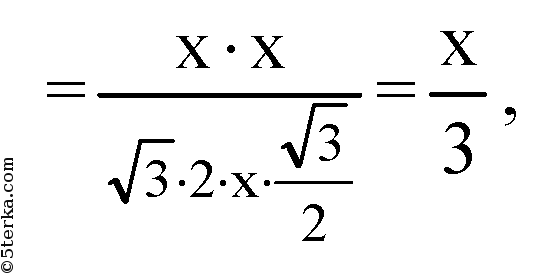
т.к.

Возвращаясь к (1), имеем:

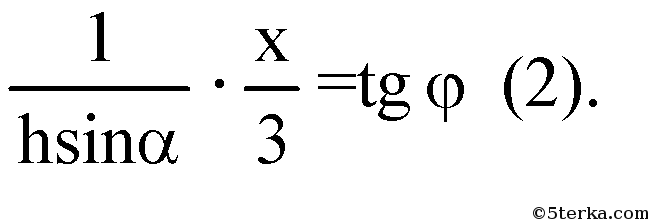
Из ΔDOC:

или

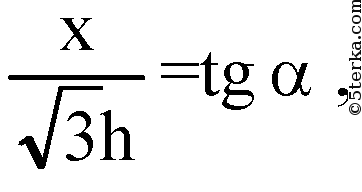
поэтому

Подставим в (2):

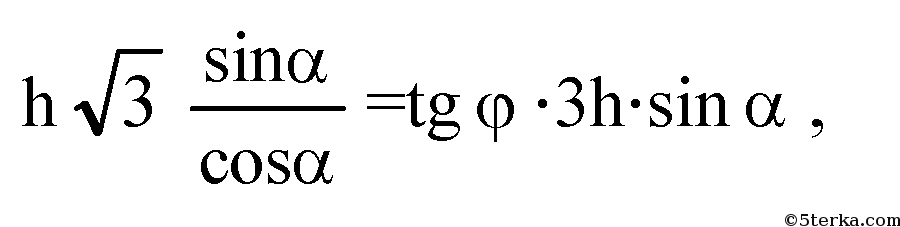
т.е.

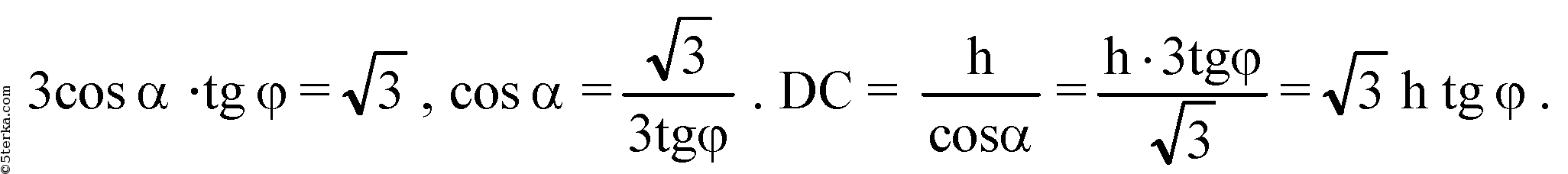
Вычислим сторону основания х:

с другой стороны, из ΔDOC: