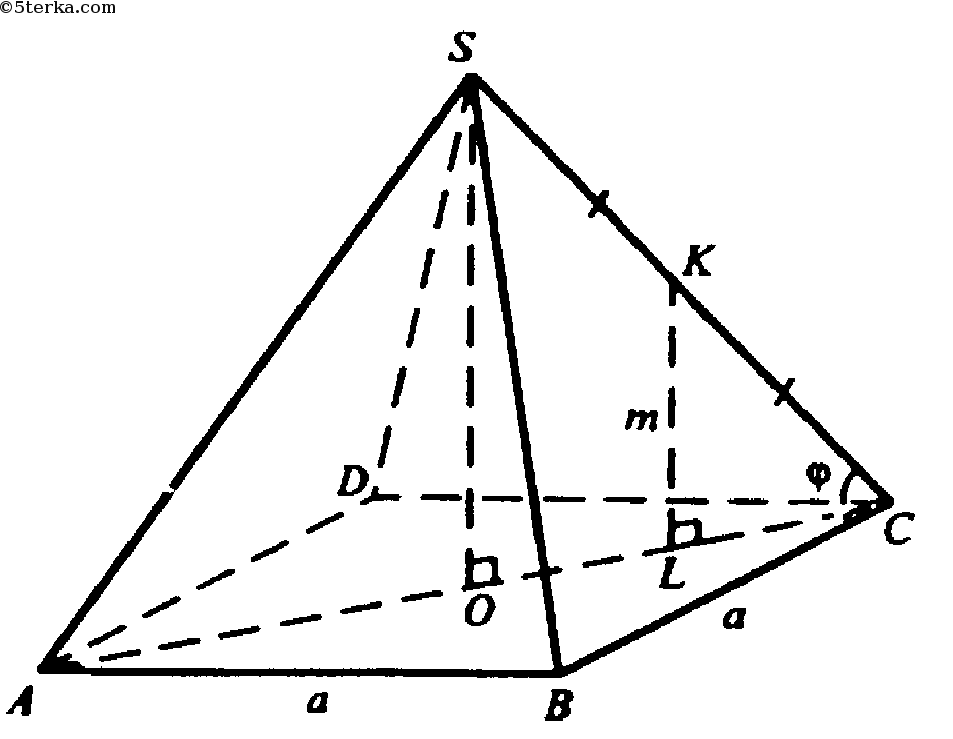
∈ плоскости SOC. KL — средняя линия в ΔSOC, значит SO=2m.

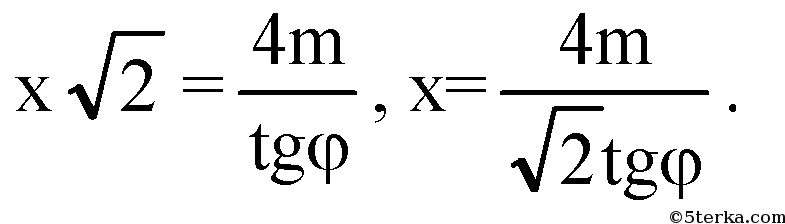
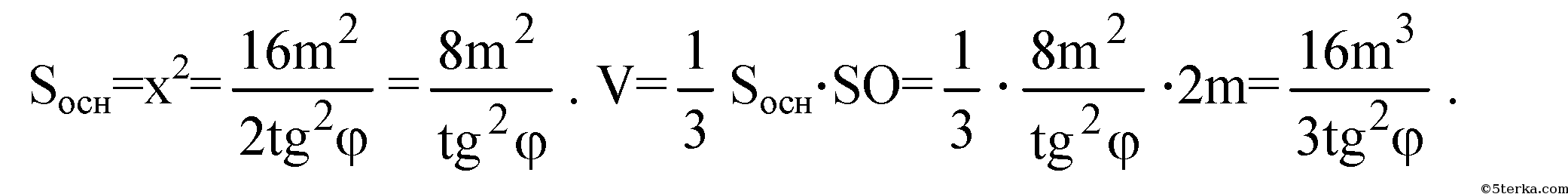
Источник:
 Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №737
к главе «Дополнительные задачи к главе VII».
Комментарии