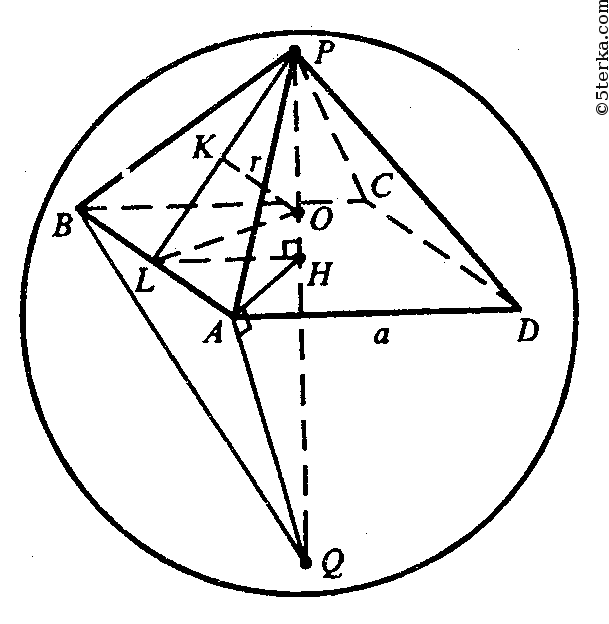
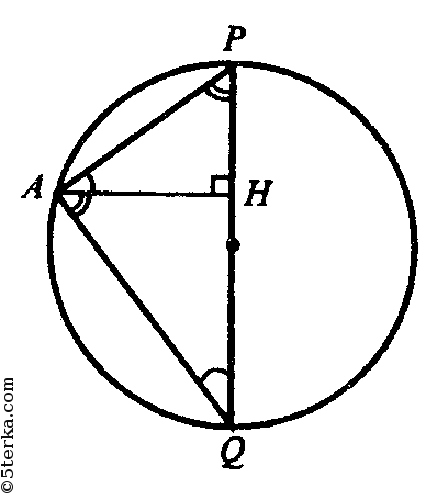
∠QAP=90° так как опирается на диаметр, Из подобия ΔHPA и ΔHAQ ,
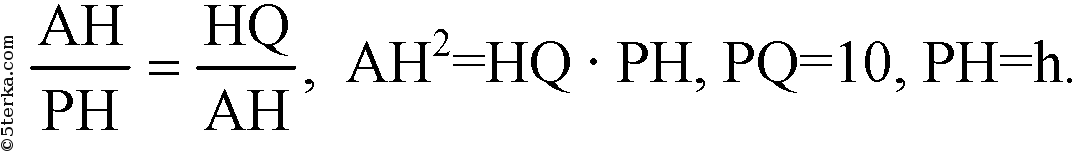
Примем х — сторона основания, следовательно,
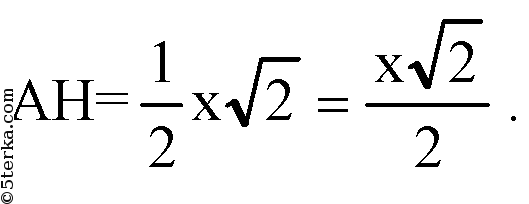
Следовательно,
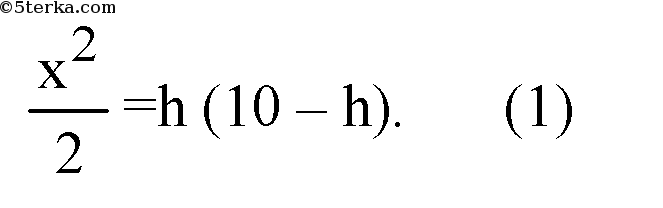
Построим HL ⊥ AB, отрезок PL.
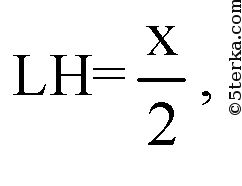
плоскость PLH ⊥ плоскости
АВР. Пусть О — центр вписанной сферы, ОК ⊥ PL.
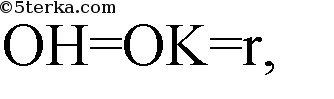
OL — биссектриса ∠HLP.
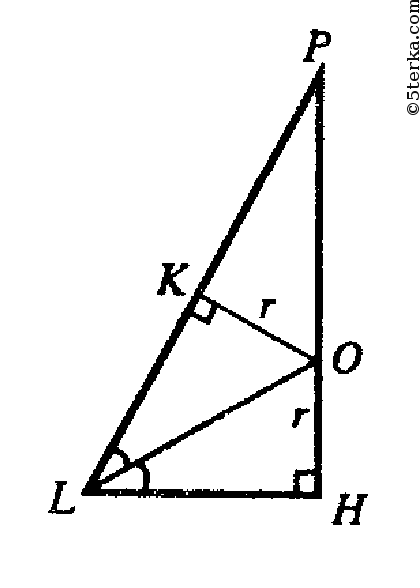
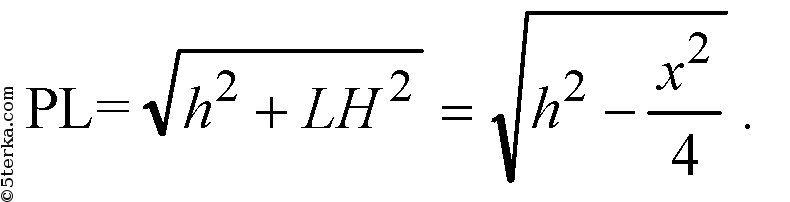
Обозначим ∠HLP= φ.
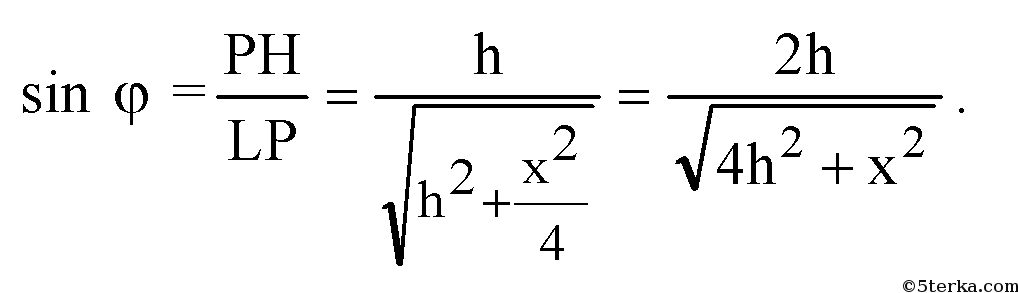
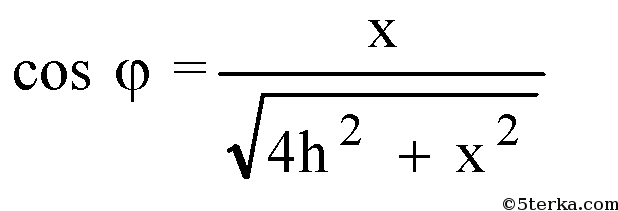
Из ΔOLH:
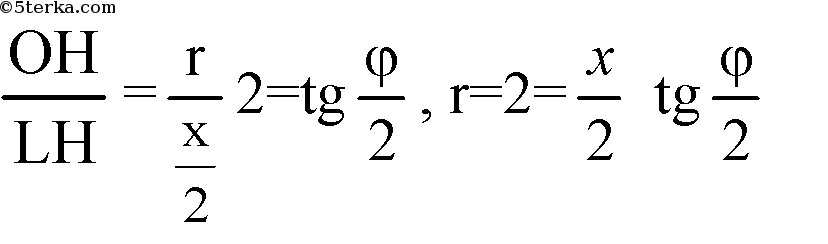
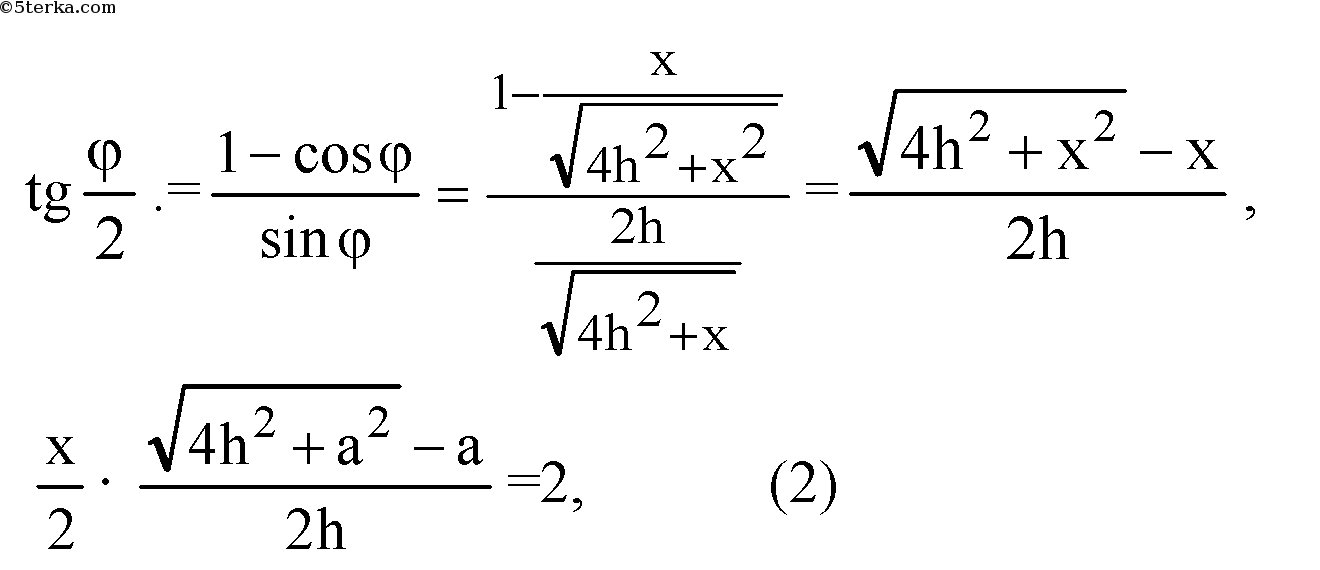
Решим систему:
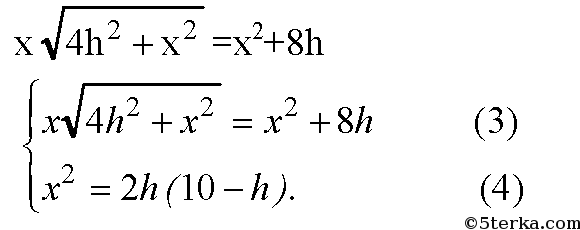
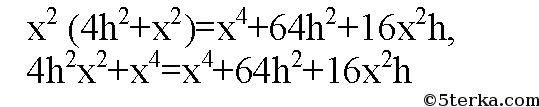
Разделим все на 4h, h ≠ 0
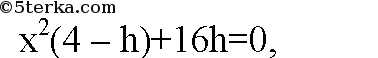
Подставим х2 из (4)
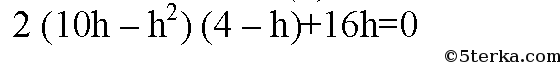
Разделим обе части на 2h, h ≠ 0
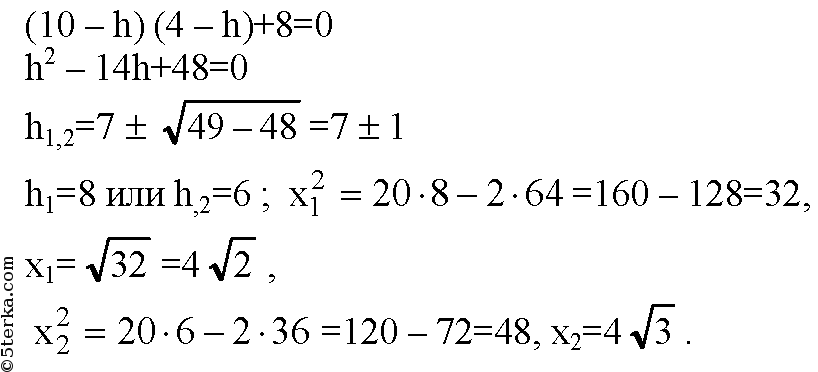
Источник:
 Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №641
к главе «Разные задачи на многогранник, цилиндр, конус и шар».
Комментарии