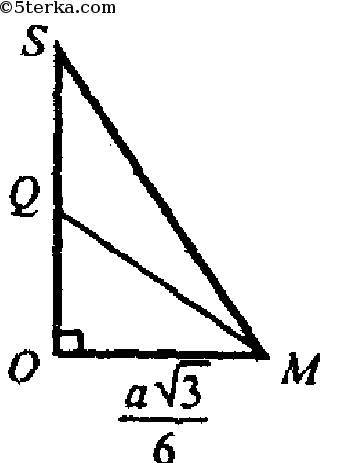
Пусть О — центр основания пирамиды, М — середина ВС, АМ — высота в ΔАВС.

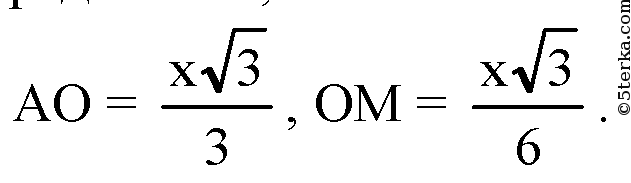
Центры обеих сфер лежат на прямой SO, SO ⊥ плоскости АВ.
Обозначим R — радиус описанной сферы. Продолжим SO до пересечения с описанной сферой в точке D. SD — диаметр шара, ∠SAD=90°. Из подобия треугольников OAS и ODA:
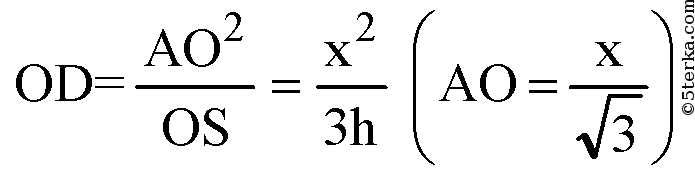
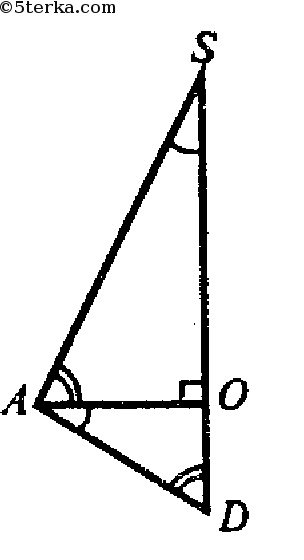
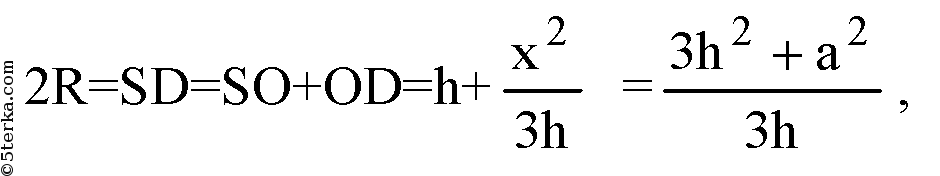
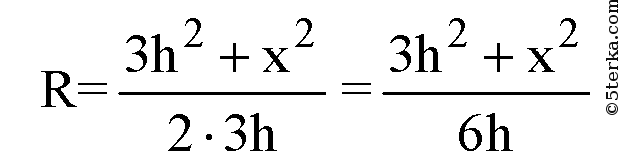
Проведем апофему SM.
Из ΔSMC:
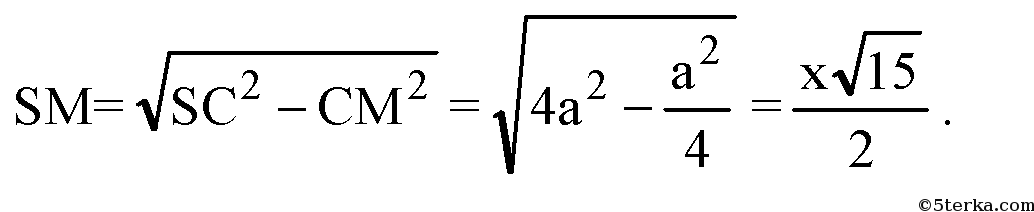
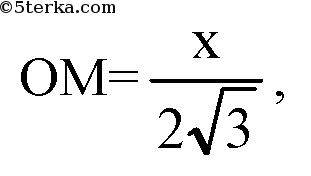
поэтому из ΔSOM:

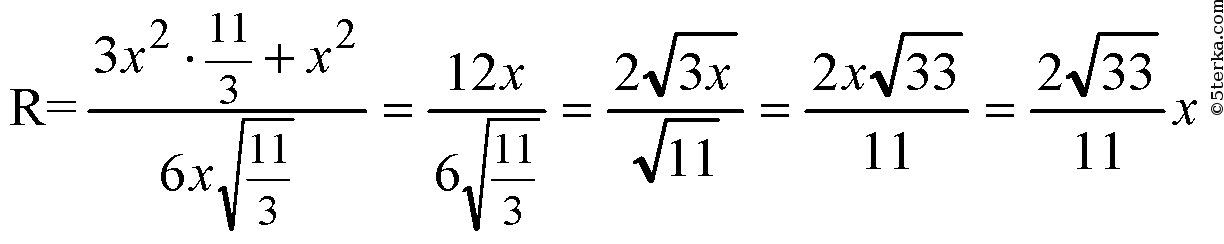
Вычислим радиус г вписанной сферы.
Примем Q — центр вписанного шара, следовательно в
ΔSOM; QM — биссектриса ∠SMO;
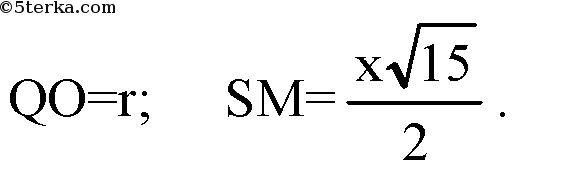
По свойству биссектрисы внутреннего угла треугольника:
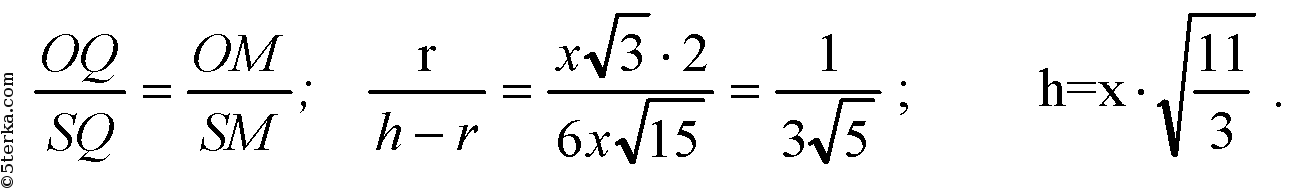
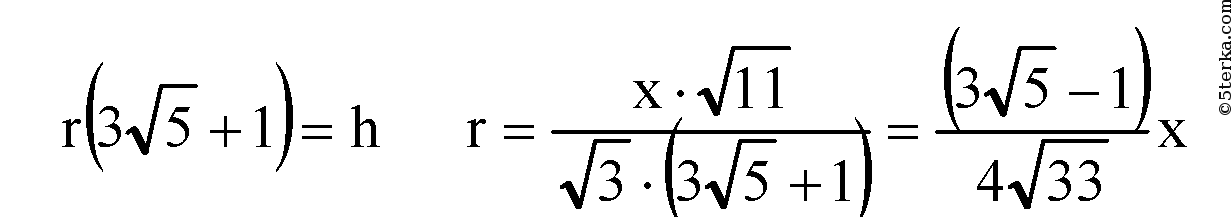
Источник:
 Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №640
к главе «Разные задачи на многогранник, цилиндр, конус и шар».
Комментарии