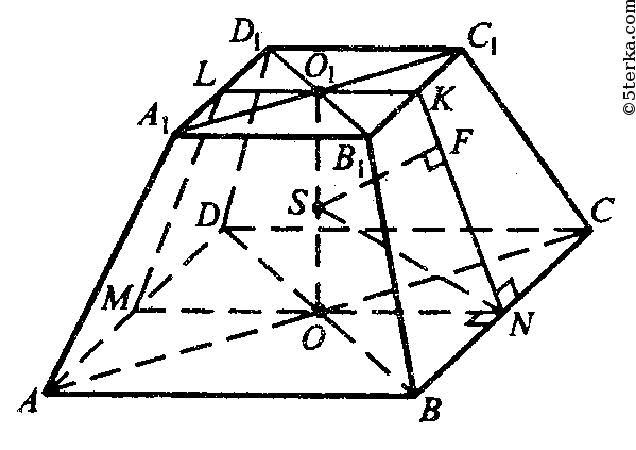
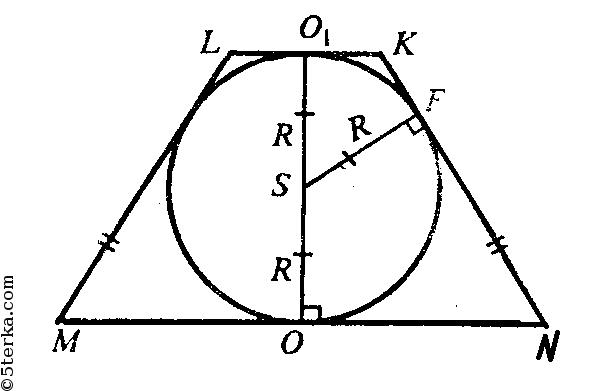
636. Докажите, что если в правильную усеченную четырехугольную пирамиду можно вписать сферу, то апофема пирамиды равна полусумме сторон оснований ее боковой грани.

Боковые грани — это равнобедренные трапеции.

В правильной усеченной пирамиде, центр вписанной в нее сферы лежит на середине отрезка ОО1 где О и О1 — центры оснований. Это следует из теоремы о центре сферы вписанной в правильную пирамиду. (см. задачу № 633).

В описанном четырехугольнике суммы противоположных сторон равны.

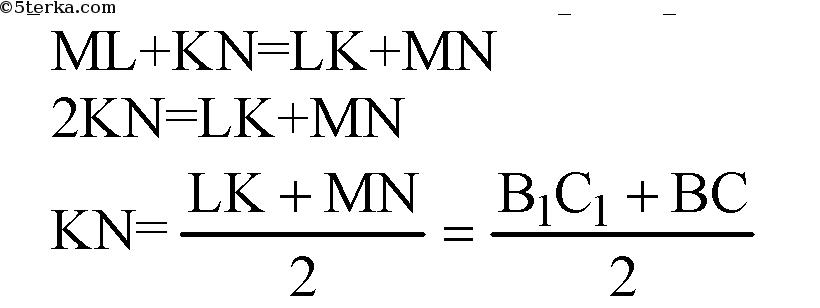
(в основаниях —

квадраты,

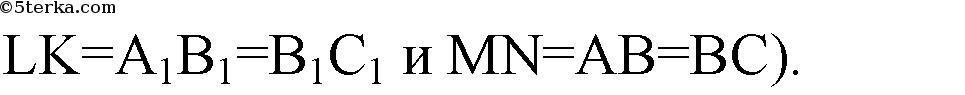
Доказано.

Источник:

Решебник по геометрии за 10 класс к учебнику Геометрия. 10-11 класс Л.С.Атанасян Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №636
к главе «Разные задачи на многогранник, цилиндр, конус и шар».

Все задачи

← 635. Около сферы радиуса R описана правильная четырехугольная пирамида, плоский угол при вершине которой равен α. а) Найдите площадь боковой поверхности пирамиды. б) Вычислите эту площадь при R = 5 см, α = 60°.
637. Докажите, что центр сферы, описанной около: а) правильной призмы, лежит в середине отрезка, соединяющего центры оснований этой призмы; б) правильной пирамиды, лежит на высоте этой пирамиды или ее продолжении. →
Комментарии