PN⊥DC, PM ⊥ AB. Центр сферы совпадает с точкой пересечения биссектрис двугранных углов при основании: также известно, что центр сферы, вписанной в правильную пирамиду, лежит на высоте пирамиды. Значит, SN — биссектриса ∠PNO — линейный угол двугранного угла при основании пирамиды.
Обозначим
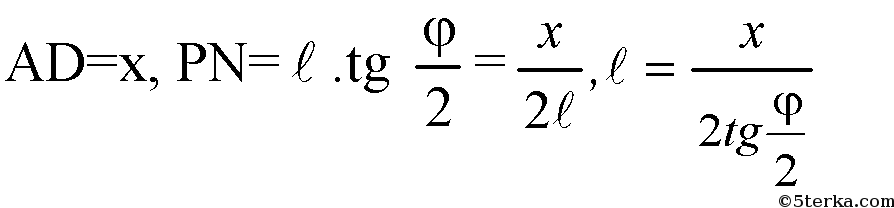
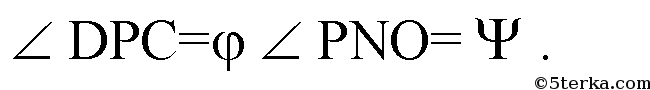
В ΔPON:
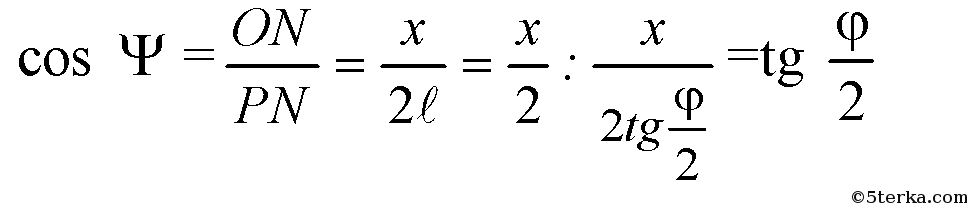
В A SON:
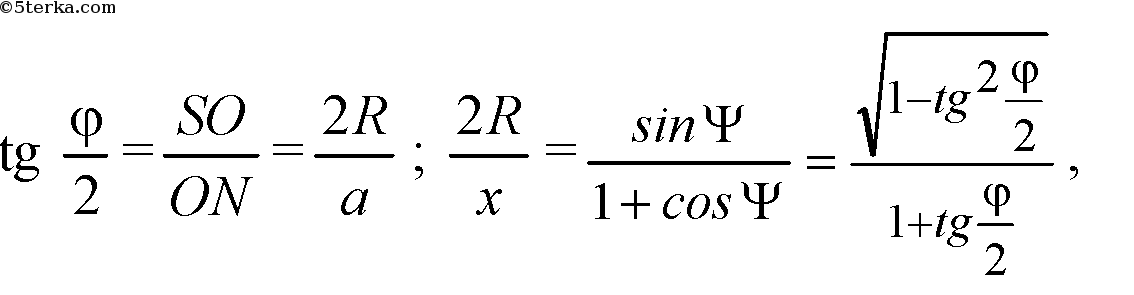
отсюда
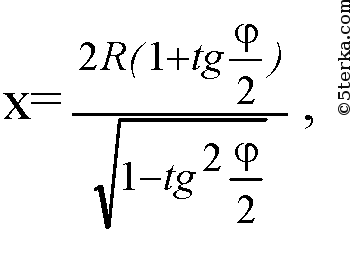
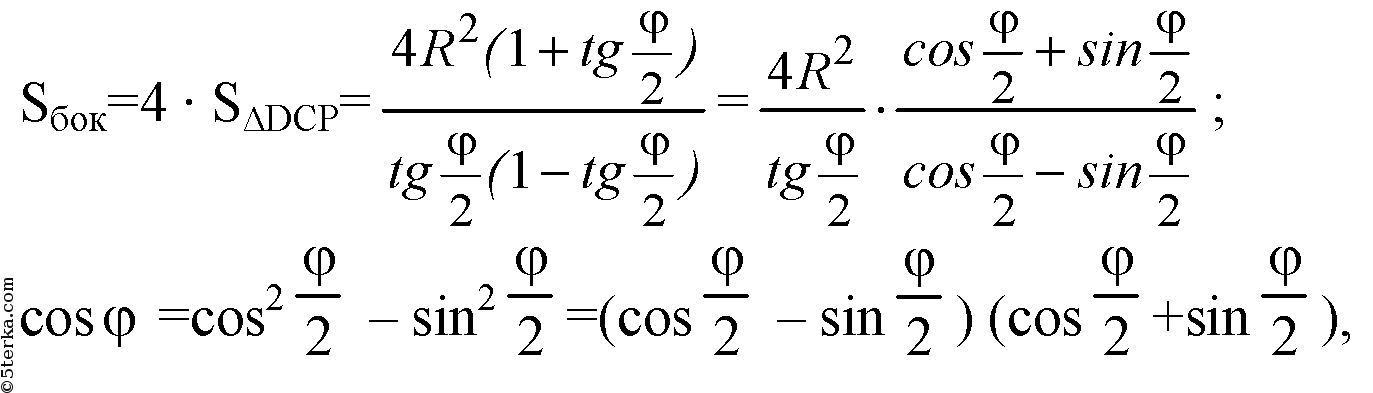
отсюда
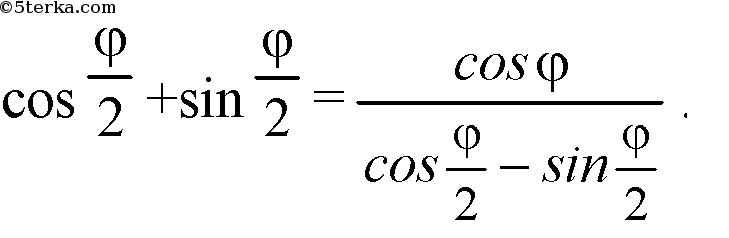
Итак,
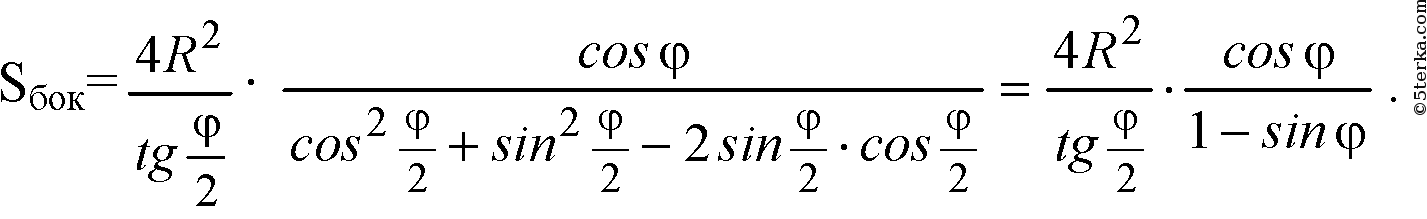
При R=5 см и φ =60 ° получим:
Источник:
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №635
к главе «Разные задачи на многогранник, цилиндр, конус и шар».
Комментарии