628. Тело ограничено двумя сферами с общим центром. Докажите, что площадь его сечения плоскостью, проходящей через центры сфер, равна площади сечения плоскостью, касательной к внутренней сфере.

Пусть R — радиус внешней сферы; г — радиус внутренней сферы. Сечение тела плоскостью, которая проходит через центры сфер, кольцо. Площадь кольца равна

Сечение, плоскостью касательной к внутренней сфере — окружность.

По теореме п. 61 ОС=r перпендикулярен к плоскости в сечении. Из прямоугольного ΔАСО:

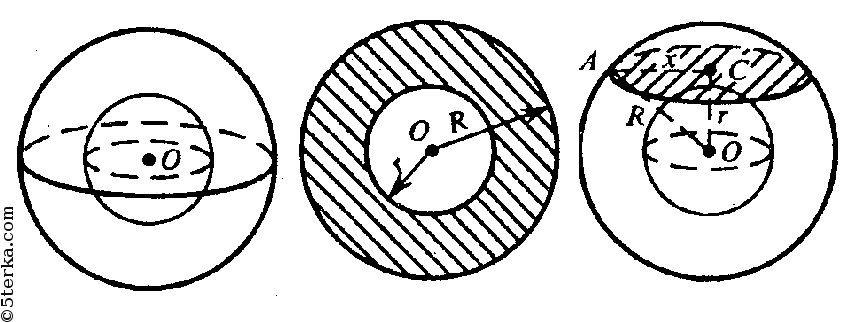
Сравнивая выражение (1) и (2) тождественны, убеждаемся в справедливости утверждения задачи.