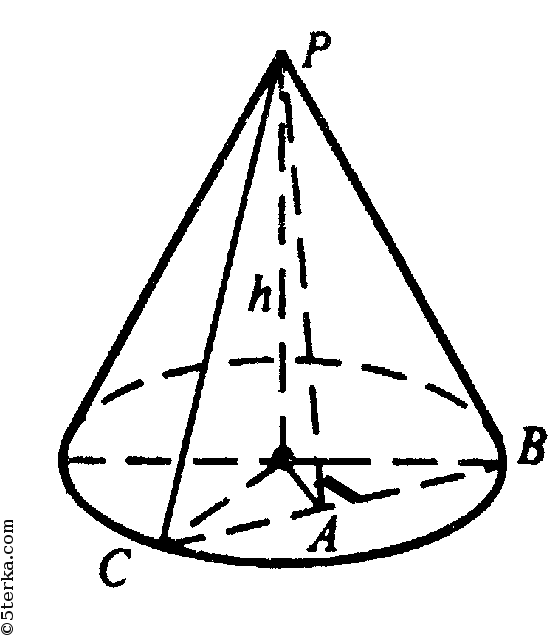
∠COB = 60°, двугранный угол между плоскостью основания и плоскостью ВРС равен: а) 30°; б) 45°; в) 60°. SBPC = ?
Построим линейный угол данного двугранного угла. Проводим ОА ⊥ ВС,
строим отрезок РА. По теореме о трех перпендикулярах РА⊥ВС.
OA⊥BC, PO⊥PAO, поэтому ∠РАO — линейный угол двугранного угла.
а) ∠РАО=30o. Из ΔРОА:
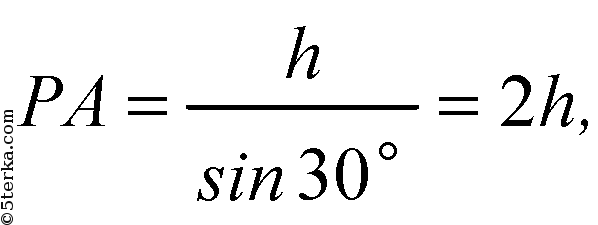
из
ΔСОВ:
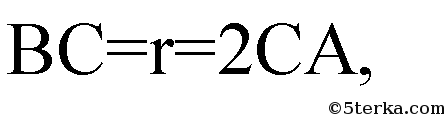
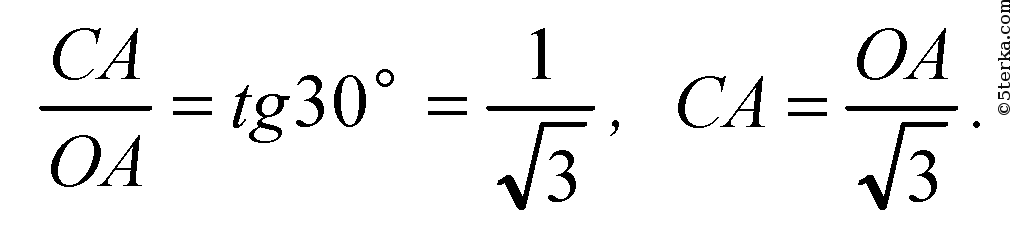
Из ΔРОА:
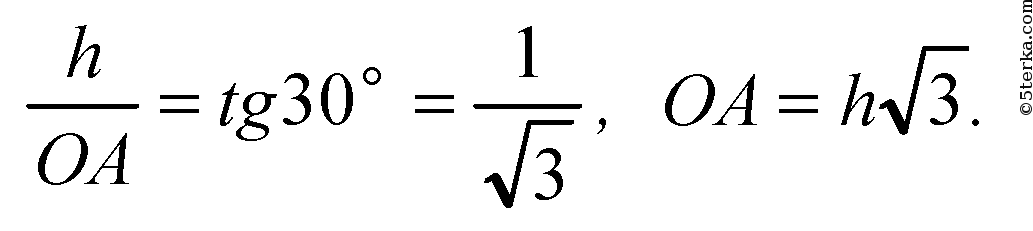
Итак,
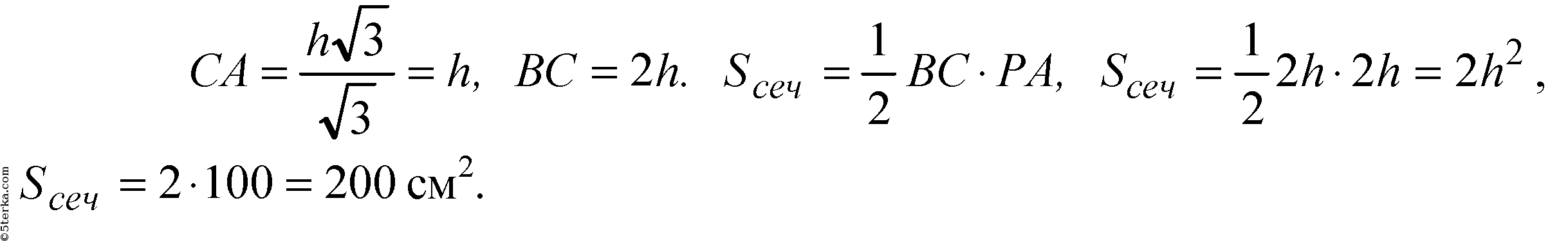
б) ∠РАО= 45°.
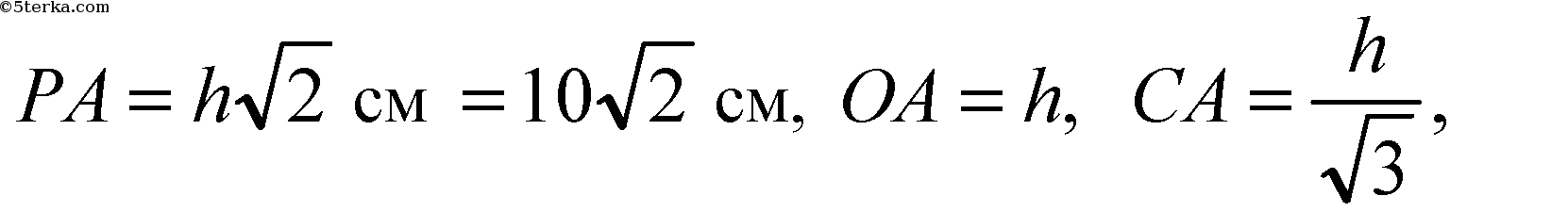
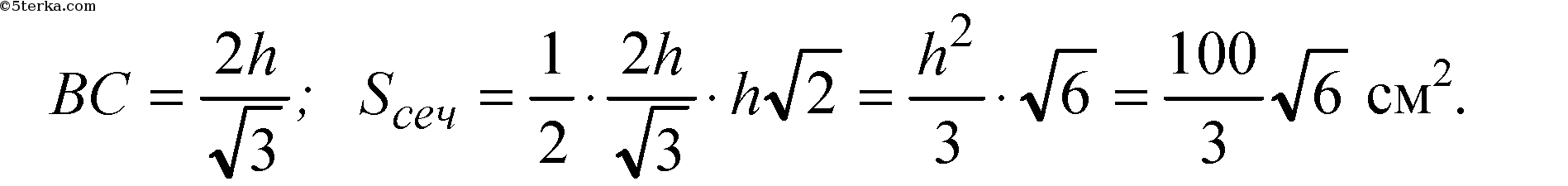
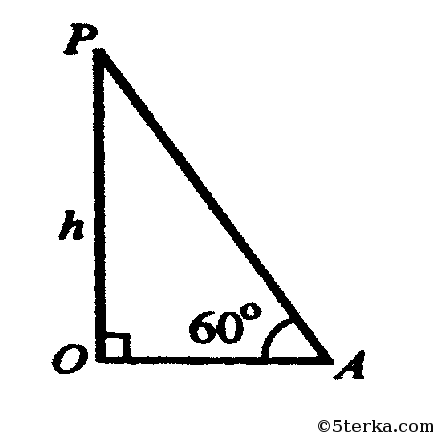
в) ∠PAO = 60°;
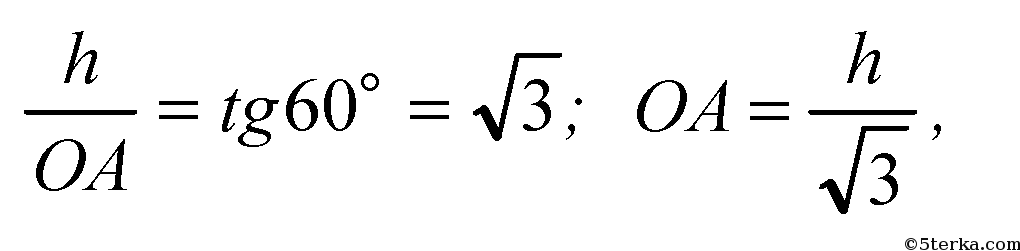
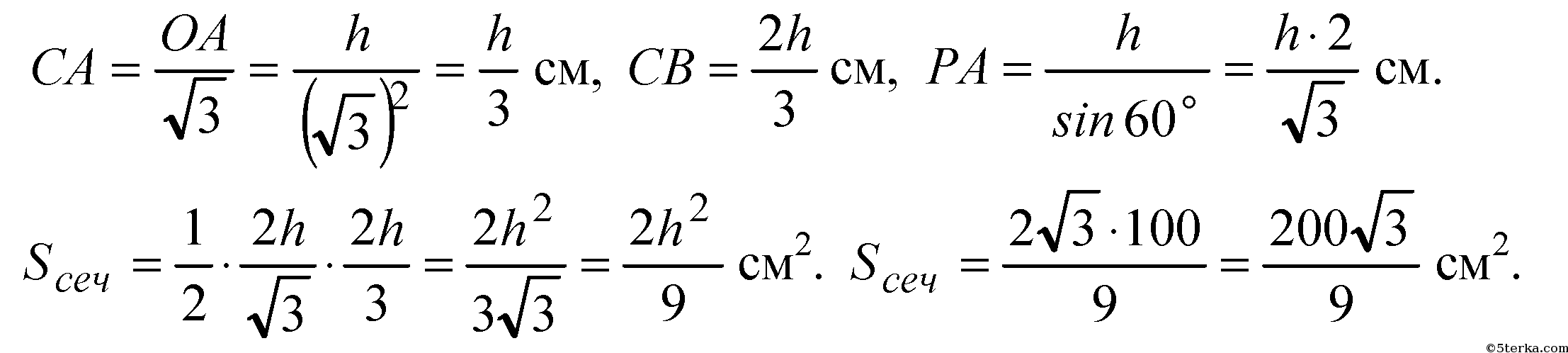
Источник:
 Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №555
к главе «Глава VI. Цилиндр, конус и шар § 2. Конус».
Комментарии