Из А проведем прямую ОА ⊥ АВ, ∠CAO=φ. Отложим АС=АО; построим отрезок СО, из точки О проведем луч, пересекающий луч AD в точке D, OD || АВ.
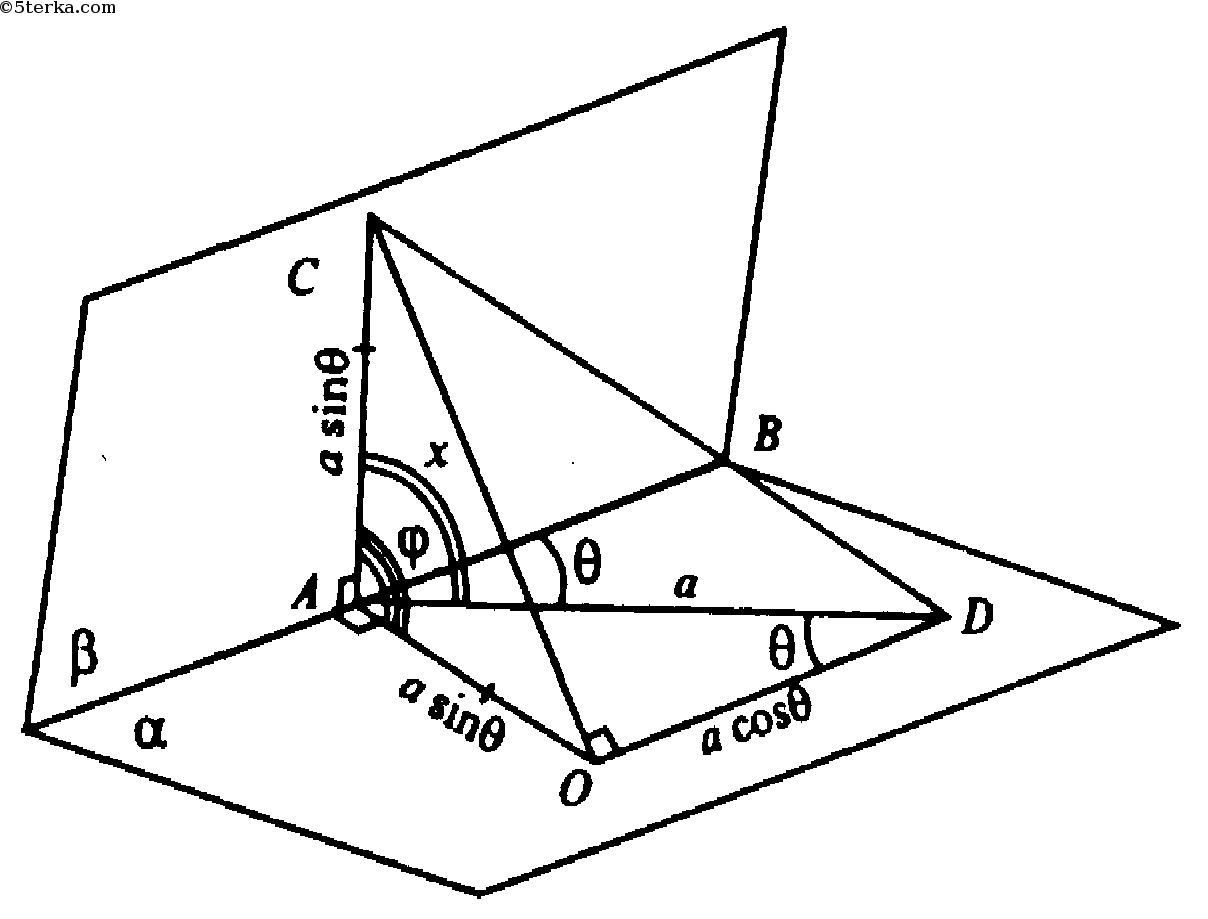
OD || АВ, а ОА ⊥ АВ, значит, OD ⊥ OA. По теореме о трех перпендикулярах: CO⊥OD.
Обозначим AD=а. Тогда в ΔAOD: AO=a sin Θ, OD=a cos Θ.
Из ΔOАС по теореме косинусов:
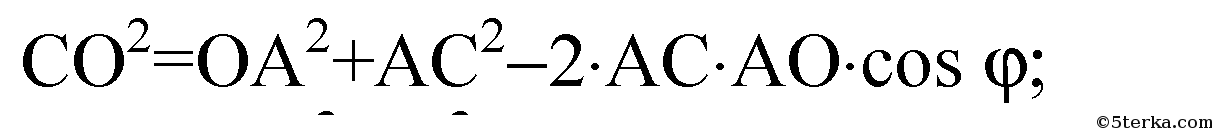
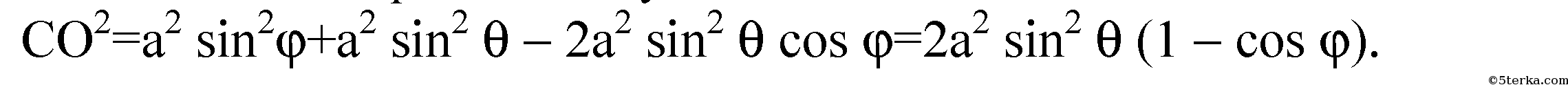
В прямоугольном ΔCOD
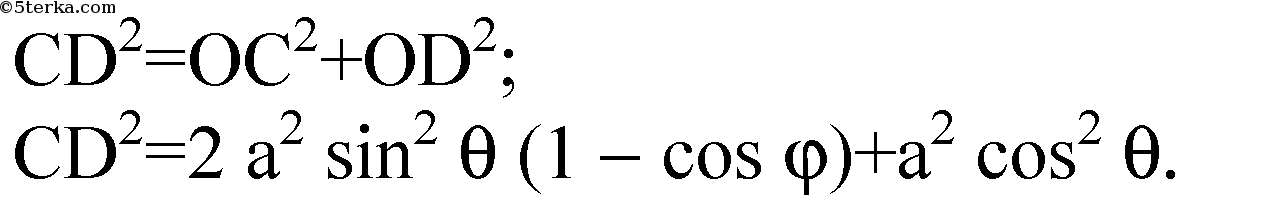
В ΔCAD по теореме косинусов искомый ∠CAD=х;
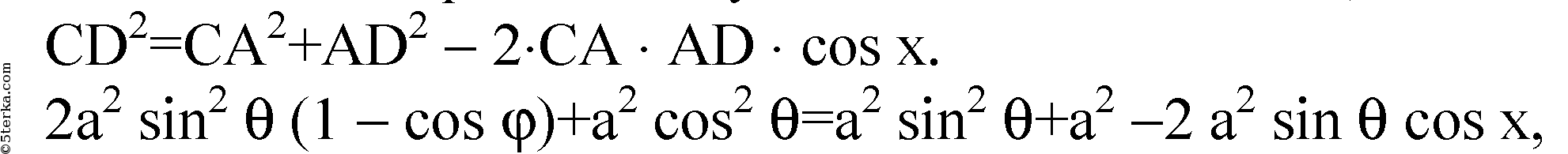
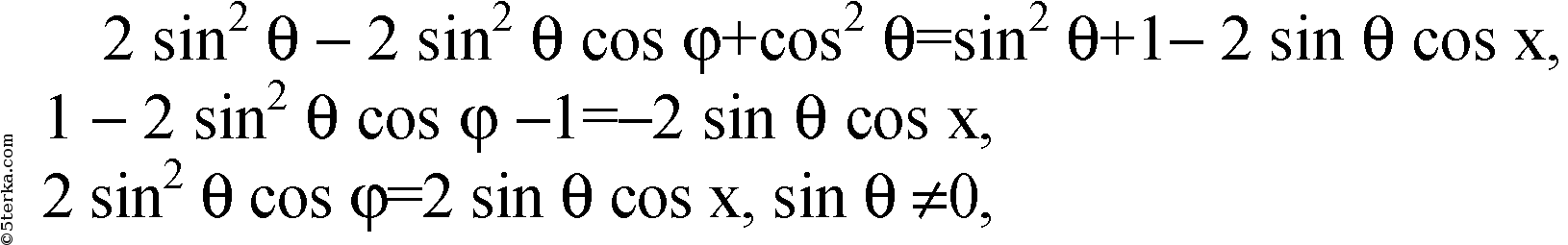
следовательно,
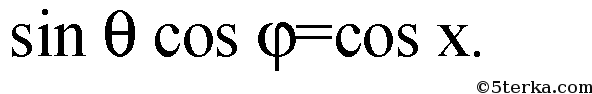
Источник:
 Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №516
к главе «Дополнительные задачи к главе V Метод координат в пространстве».
Комментарии