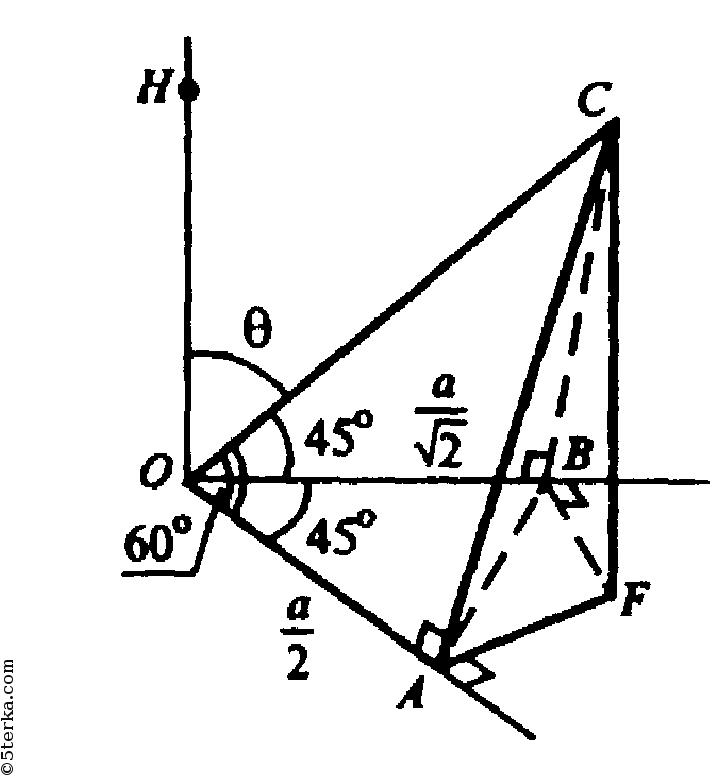
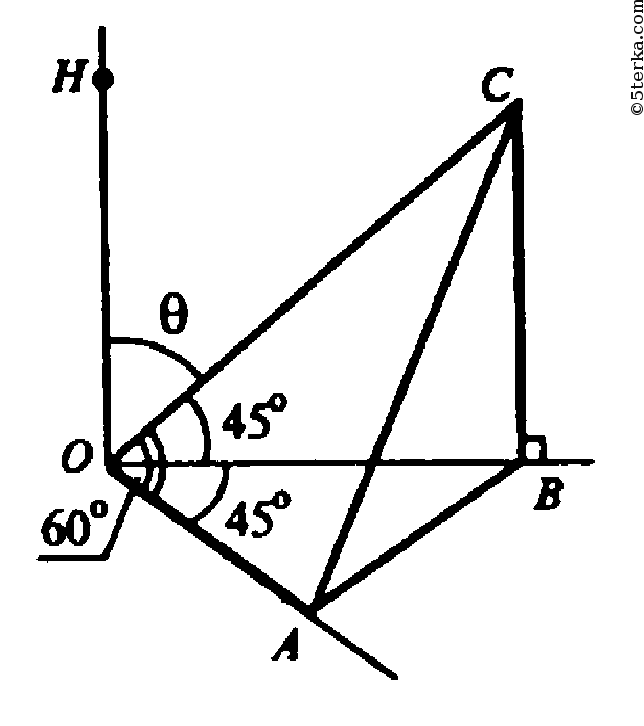
Из точки С проведем прямую CF перпендикулярную плоскости АОВ, в плоскости АОВ проведем FA ⊥ ОА, FB ⊥ ОВ. По теореме о трех перпендикулярах: СА ⊥ ОА и СВ ⊥ ОВ. Пусть ОС=а, тогда из ΔСOА:
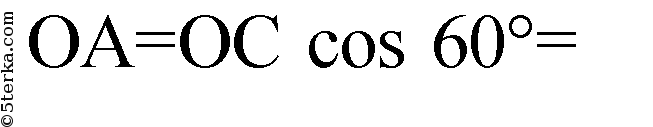
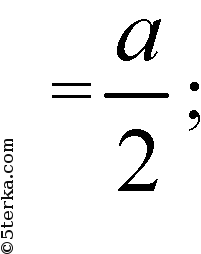
из ΔCOB:
Для ΔАOВ по теореме косинусов:
Таким образом, ΔAOB — равнобедренный, ОА=АВ; ∠АВO=45°, ∠OАВ=90°.
Тогда, FA совпадает с АВ и С проектируется в точку В.
Прямые НО и СВ перпендикулярны к плоскости АВО, т.е. они лежат в одной плоскости, ∠НOВ=90°, ∠COB=45°, таким образом, искомый угол Θ=45°.
Источник:
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №515
к главе «Дополнительные задачи к главе V Метод координат в пространстве».
Комментарии